FINDING THE DISTANCE BETWEEN TWO POINTS

The Pythagorean Theorem can be used to find the distance between any two points (x₁, y₁) and (x₂, y₂) in the coordinate plane. The resulting expression is called the Distance Formula.

In a coordinate plane, the distance d between two points (x₁, y₁) and (x₂, y₂) is

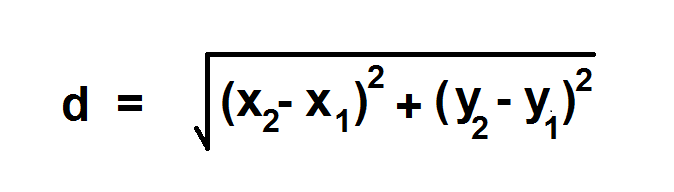
Using the Pythagorean Theorem to derive the Distance Formula

Step 1 :

To find the distance between points P(x₁, y₁) and Q(x₂, y₂), draw segment PQ and label its length d. Then draw horizontal segment PR and vertical segment QR . Label the lengths of these segments a and b.

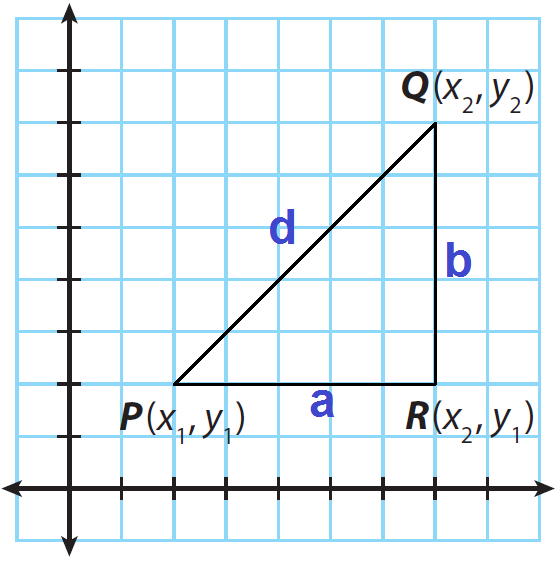
PQR is a right triangle with hypotenuse PQ  =  d.  

Step 2 :

Since PR is a horizontal segment, its length, a, is the difference between its x-coordinates. Therefore,

a  =  x₂ - x₁

Step 3 :

Since QR is a horizontal segment, its length, b, is the difference between its y-coordinates. Therefore,

b  =  y₂ - y₁

Step 4 :

Use the Pythagorean Theorem to find d, the length of segment PQ. Substitute the expressions from step 2 and step 3 for a and b. 

d²  =  a² + b²

Thus, we have

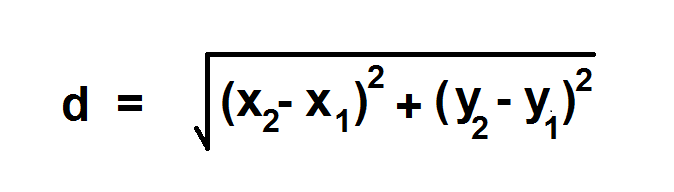
Reflect

Why are the coordinates of point R the ordered pair (x₂, y₁) ?

Since R lies on the same vertical line as Q, their x-coordinates are the same. Since R lies on the same horizontal line as P, their y-coordinates are the same.

Practice Problems

Problem 1 :

Find the distance between the points A(-12, 3) and B(2, 5).

Solution:

Step 1 :

Write the formula to find the distance between the two points A(-12, 3) and B(2, 5).

AB  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

Step 2 :

Substitute x₁ = -12, y₁ = 3, x₂ = 2, and y₂ = 5.

AB  =  √[(2 + 12)² + (5 - 3)²]

AB  =  √(14² + 2²)

AB  =  √(196 + 4)

AB  =  √200

AB  =  √(2 x 10 x 10)

AB  =  10√2 units

Problem 2 :

Find the distance between the points P(-2, -3) and Q(6, -5).

Solution:

Step 1 :

Write the formula to find the distance between the two points P(-2, -3) and Q(6, -5).

PQ  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

Step 2 :

Substitute x₁ = -2, y₁ = -3, x₂ = 6, and y₂ = -5.

PQ  =  √[(6 + 2)² + (-5 + 3)²]

PQ  =  √(8² + (-2)²]

PQ  =  √(64 + 4)

PQ  =  √68

PQ  =  √(2 x 2 x 17)

PQ  =  2√17 units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.