FINDING THE INDICATED TERM OF A SEQUENCE

Question 1 :

Find the indicated terms of the sequences whose nth terms are given by

(i) a_n  =  5n / (n + 2); a₆ and a₁₃

Solution :

To find a₆, we have to apply 6 instead of n.

To find a₁₃, we have to apply 13 instead of n.

(ii) a_n  =  -(n² - 4); a₄ and a₁₁

Solution :

To find a₄, we have to apply 4 instead of n.

To find a₁₁, we have to apply 11 instead of n.

Question 2 :

Find a₈ and a₁₅ whose nth term is

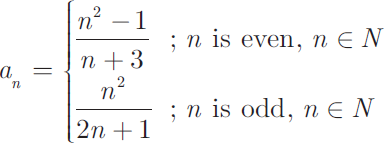
Solution :

In a_8, 8 is even in a₁₅, 15 is odd 

Question 3 :

If a₁ = 1, a₂ = 1 and a_n = 2a_{n - 1} + a_{n - 2} n ≥ 3, n ∈ N, then find the first six terms of the sequence.

Solution :

First and second terms are 1.

a_n = 2a_{n - 1} + a_{n - 2} 

Hence the first 6 terms are 1, 1, 3, 7, 17, 41.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.