FINDING THE INVERSE OF AN ELEMENT IF THE FUNCTION IS GIVEN
Question 1 :
If f -> Q -> Q is given by f(x) = x2, then find
(i) f-1 (9) (ii) f-1(-5) (iii) f-1(0)
Solution :
From the given function, we have
f(x) = x2
x = f-1(x2) ----(1)
(i) f-1 (9)
By comparing f-1 (9) with (1), we get that
x2 = 9
x = ±3
(ii) f-1(-5)
By comparing f-1 (5) with (1), we get that
x2 = -5
x = √-5 which is not possible
f-1(-5) is undefined.
(iii) f-1(0)
By comparing f-1 (0) with (1), we get that
x2 = 0
x = 0
Hence the value of f-1(0) = 0.
Question 2 :
In the function f : R-> R be defined by f(x) = x2 + 5x + 9, find f-1 (8) and f-1(9)
Solution :
Given that : f(x) = x2 + 5x + 9
x = f-1(x2 + 5x + 9) ---(1)
f-1 (8) ---(2)
By comparing (1) and (2), we have 8 instead of x2 + 5x + 9
x2 + 5x + 9 = 8
x2 + 5x + 9 - 8 = 0
x2 + 5x + 1 = 0
x = (-b±√b2 - 4ac)/2a
x = (-5±√(52-4))/2(1)
x = (-5±√21)/2
f-1(9)
x2 + 5x + 9 = 9
x2 + 5x + 9 - 9 = 0
x2 + 5x = 0
x(x + 5) = 0
x = 0 and x = -5
Question 3 :
Let R-> R be defined on f(x) = x2 + 1. Find
(i) f-1 (-5) (ii) f-1(26) (iii) f-1[10, 37]
Solution :
f(x) = x2 + 1
(i) f-1 (-5)
x2 + 1 = -5
x2 = -6 Which is not real.
(ii) f-1(26)
x2 + 1 = 26
x2 = 26 - 1
x2 = 25
x = ± 5
(iii) f-1[10, 37]
|
x2 + 1 = 10 x2 = 10 - 1 x2 = 9 x = ± 3 |
x2 + 1 = 37 x2 = 37 - 1 x2 = 36 x = ± 6 |
Hence the values of x are [-6, -3, 3, 6].
Question 4 :
Find the inverse of the relation.
(1, 0), (3, −8), (4, −3), (7, −5), (9, −1)
Solution :
Inverse relation is
(0, 1) (-8, 3) (-3, 4) (-5, 7) (-1, 9)
Question 5 :
Find the inverse of the relation.
(2, 1), (4, −3), (6, 7), (8, 1), (10, −4)
Solution :
The inverse relation is,
(1, 2) (-3, 4) (7, 6) (1, 8) (-4, 10)
Question 6 :
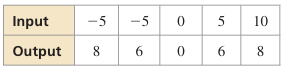
Solution :
Writing the ordered pairs from the table, we get
(-5, 8) (-5, 6) (0, 0) (5, 6) (10, 8)
The inverse relation is,
(8, -5) (6, -5) (0, 0) (6, 5) (8, 10)
Use the tables below to find the given values.
Question 7 :
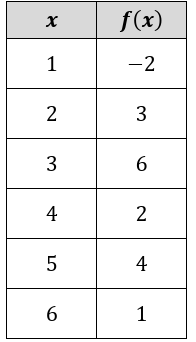
|
a. 𝑓(1) b. 𝑓(6) c. 𝑓-1 (1) |
d. 𝑓-1 (4) e. 𝑓 (2) f. 𝑓-1 (6) |
Solution :
a. 𝑓(1)
When the input is 1, the output is -2.
b. 𝑓(6)
When the input is 6, the output is 1.
c. 𝑓-1 (1)
When the output is 1, the input is 6.
d. 𝑓-1 (4)
When the output is 4, the input is 5.
e. 𝑓 (2)
When the input is 2, the output is 3.
f. 𝑓-1 (6)
When the input is 6, the output is 3.
Question 8 :
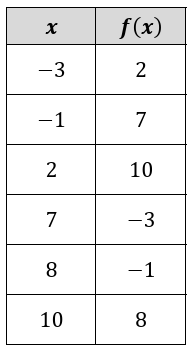
|
a. 𝑓(2) b. 𝑓(10) c. 𝑓-1 (7) |
d. 𝑓-1 (-3) e. 𝑓(7) f. 𝑓-1 (2) |
Solution :
a. 𝑓(2) :
When the input is 2, the output is 10.
b. 𝑓(10) :
When the input is 10, the output is 8.
c. 𝑓-1 (7) :
When the output is 7, the input is -1.
d. 𝑓-1 (-3) :
When the output is -3, the input is 7.
e. 𝑓(7) :
When the input is 7, the output is -3.
f. 𝑓-1 (2) :
When the output is 2, the input is -3.
Question 10 :
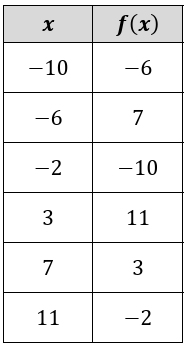
|
a. 𝑓(-10) b. 𝑓(3) c. 𝑓-1 (7) |
d. 𝑓-1 (-6) e. 𝑓(7) f. 𝑓-1 (-2) |
Solution :
a. 𝑓(-10) :
When the input is -10, the output is -6.
b. 𝑓(3) :
When the input is 3, the output is 11.
c. 𝑓-1 (7) :
When the input is 7, the output is 3.
d. 𝑓-1 (-6) :
When the output is -6, the input is -10.
e. 𝑓(7) :
When the input is 7, the output is 3.
f. 𝑓-1 (-2) :
When the output is -2, the input is 11.
Question 11 :
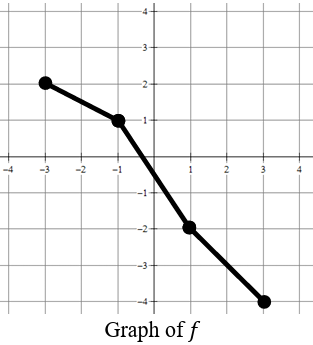
The graph of the piecewise-linear function 𝑓 is shown in the figure. Let 𝑔 be the inverse function of 𝑓. What is the minimum value of 𝑔?
a) -4 b) -3 c) 2 d) 3
Solution :
Functions f and g are inverse to each other. The minimum value of f from the above graph is (3, -4)
Set of ordered pairs from graph of f are,
(-3, 2) (-1, 1) (1, -2) (3, -4)
Set of ordered pairs from graph of g are,
(2, -3) (1, -1) (-2, 1) (-4, 3)
At (2, -3) we have the minimum point. So, the answer is -3.
Question 12 :
Mr. Brust is filling up his backdoor kiddie pool with the water hose. The amount of water, in gallons, in the pool 𝑡 minutes after he turns on the water can be modeled by 𝑃, an increasing function of time 𝑡. Which of the following gives a verbal representation of the function 𝑃-1 , the inverse of 𝑃?
a) 𝑃-1 is an increasing function of the amount of time after the water is turned on.
b) 𝑃-1 is a decreasing function of the amount of time after the water is turned on.
c) 𝑃-1 is an increasing function of the amount of water in the pool.
d) 𝑃-1 is a decreasing function of the amount of water in the pool.
Solution :
Accordingly the function P :
- Dependent variable = time
- Independent variable = Amount of water in gallons.
Accordingly inverse function of 𝑃-1 :
- Independent variable = time
- Dependent variable = Amount of water in gallons.
So, option a is correct.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
