FINDING THE MEASURE OF THE REFERENCE ANGLE

Example 1 :

What is the reference angle for each angle in standard position? 

(a)   170°      (b)   345°     (c)   72°   (d)   215°

Solution :

(a) 170°

Since the given angle lies in second quadrant, the reference angle of 170 is 180 - 170. That is 10°.

(b) 345°

Since the given angle lies in fourth quadrant, the reference angle of 345 is 360 - 345. That is 15°.

(c) 72°  

Since the given angle lies in first quadrant, the reference angle is 72°.

(d) 215°

Since the given angle lies in third quadrant, the reference angle of 215 is 215 - 180. That is 35°.

Example 2 :

Determine the measure of the three other angles in standard position, 0° < θ < 360°, that have a reference angle of

(a) 45°       (b) 60°       (c) 30°       (d) 75°

Solution :

Let θ be given angle.

The given angle lies in first quadrant. Reference angle

= 90 - 45

θ_R = 45

Angle in the second quadrat = 180 - θ_R

= 180 - 45

= 135°

Angle in third quadrant = 180 + θ_R

= 180 + 45

= 225°

Angle in fourth quadrant = 360 - θ_R

= 360 - 45

= 315°

So, the required angles are 135°, 225° and 315°.

(b) 60°  

Solution :

Let θ be given angle.

The given angle lies in first quadrant. Reference angle

= 90 - 60

θ_R = 30

Angle in the second quadrat = 180 - θ_R

= 180 - 30

= 150°

Angle in third quadrant = 180 + θ_R

= 180 + 30

= 210°

Angle in fourth quadrant = 360 - θ_R

= 360 - 30

= 330°

So, the required angles are 150°, 210° and 330°.

(c) 30°  

Solution :

Let θ be given angle.

Required angle in 2^nd quadrant  =  180 - θ 

=  180 - 30  =  150

Required angle in 3^rd quadrant  =  180 + θ 

  =  180 + 30  =  210

Required angle in 4^th quadrant  =  360 - θ 

  =  360 - 30  =  330

Hence the required angles are 150, 210 and 330.

(d) 75°  

Solution :

Let θ be given angle.

Required angle in 2^nd quadrant  =  180 - θ 

=  180 - 75  =  105

Required angle in 3^rd quadrant  =  180 + θ 

  =  180 + 75  =  255

Required angle in 4^th quadrant  =  360 - θ 

  =  360 - 75  =  285

Hence the required angles are 105, 255 and 285.

Example 3 :

Sketch each angle in standard position, then identify the reference angle.

a)  460°       b)  -350°        c) 695°     d)  -500°

Solution :

a)  460° 

460 = 360 + 100

From this, we understand that the co-terminal angle lies in second quadrant.

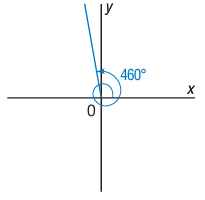
Co-terminal angle = 460° - 360°

= 100°

Reference angle lies in 2nd quadrant, then 

= 180 - 100

= 80°

b)  -350° 

-350 = -270 - 80

Since the given angle is negative, we go for counterclockwise rotation. Co-terminal angle lies in first quadrant.

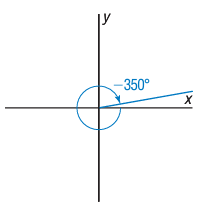
Co-terminal angle = 360° - 350°

= 10°

Reference angle is also 10°.

c)  695°

695 = -720 + 695

The angle lies in fourth quadrant. Co-terminal angle 

= -25°

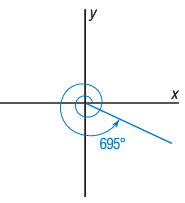
Reference angle = 25°

d)  -500°

-500 = -360 - 140

= -140°

Since the given angle is negative, we go for counterclockwise rotation. Co-terminal angle lies in third quadrant.

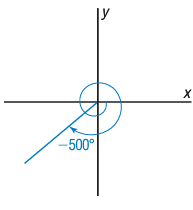
Reference angle = 140 - 270

Example 4 :

A windshield wiper has a length of 50 cm. The wiper rotates from its resting position at 30°, in standard position, to 150°. Determine the exact horizontal distance that the tip of the wiper travels in one swipe.

Solution :

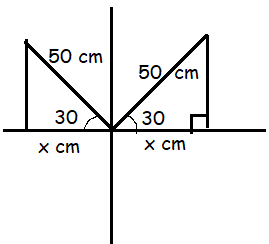
cos θ = adjacent side / hypotenuse

cos 30 = x/50

0.866 = x/50

x = 0.866(50)

x = 43.3

Required length = 2x

= 2(43.3)

= 86.6

So, the required horizontal distance is 86.6 cm.

Example 5 :

Find the values of the following trigonometric ratios :

i) sin 315     ii) cos 210    iii) cos (-480)     iv)  sin (-1125)

Solution :

i) sin 315

The given angle is in fourth quadrant. Since the given trigonometric ratio is sin, we use the negative sign.

Finding reference angle :

= 360 - 315

= 45

sin 315 = - sin 45

= 1/√2

ii) cos 210

The given angle is in third quadrant. Using ASTC, since the given trigonometric ratio is cos θ, we use the negative sign.

Finding reference angle :

= Given angle - 180

= 210 - 180

= 30

cos 210 = - cos 30

= -√3/2

iii) cos (-480)

cos (-480) = cos 480

480 = 360 + 120

The given angle is in second quadrant. Using ASTC, since the given trigonometric ratio is cos θ, we use the negative sign.

Finding reference angle :

= 180 - Given angle

= 180 - 120

= 60

cos 480 = -cos 60

= -1/2

iv)  sin (-1125)

sin (-1125) = -sin 1125

= -sin (1080 + 45) 

= -sin 45

The given angle is in first quadrant. Using ASTC, since the given trigonometric ratio is sin θ, we use the positive sign.

= - sin 45

= -1/√2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.