FINDING THE SQUARE ROOT OF A POLYNOMIAL BY LONG DIVISION METHOD

Question 1 :

Find the square root of the following polynomials by division method

(i)  x⁴ −12x³ + 42x² −36x + 9

Step 1 :

x⁴ has been decomposed into two equal parts x² and x².

Step 2 :

Multiplying the quotient (x²) by 2, so we get 2x². Now bring down the next two terms -12x³ and 42x².

By dividing -12x³ by 2x², we get -6x.  By continuting in this way, we get the following steps.

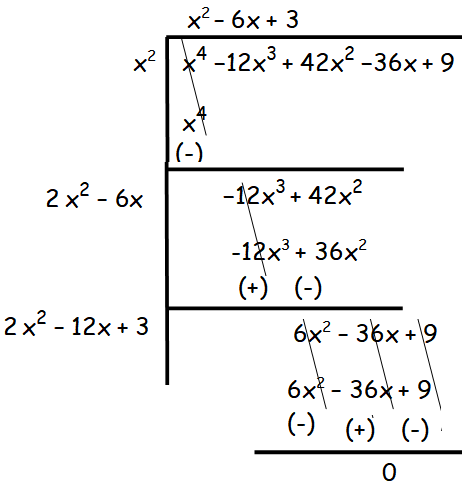
Hence the square root of  x⁴ −12x³ + 42x² −36x + 9 is x² - 6x + 3

(ii) 37x² −28x³ + 4x⁴ + 42x + 9

Solution :

First let us arrange the given polynomial from greatest order to least order.

4x⁴  −28x³ + 37x² + 42x + 9

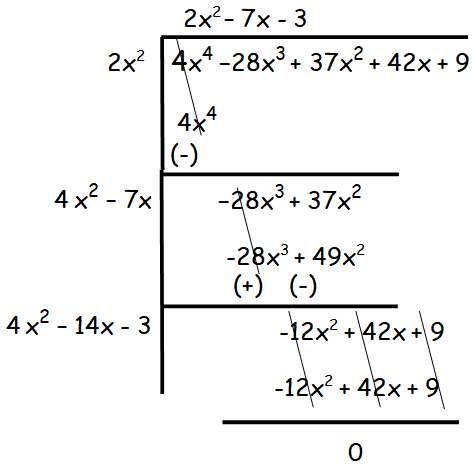
Hence the square root of  37x² −28x³ + 4x⁴ + 42x + 9 is 2x² - 7x - 3.

(iii) 16x⁴ + 8x² + 1

Solution :

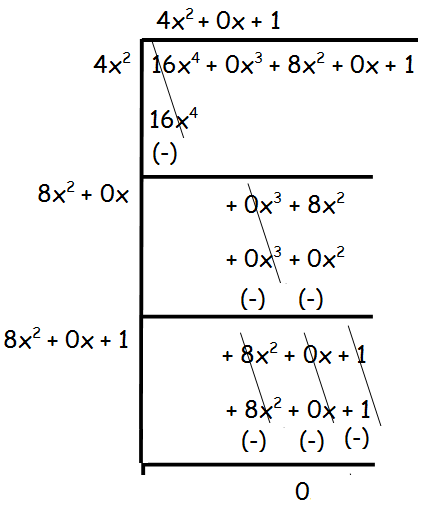
Hence the square root of  37x² −28x³ + 4x⁴ + 42x + 9 is 4x² + 0x + 1.

(iv) 121x⁴ − 198x³ − 183x² + 216x + 144

Solution :

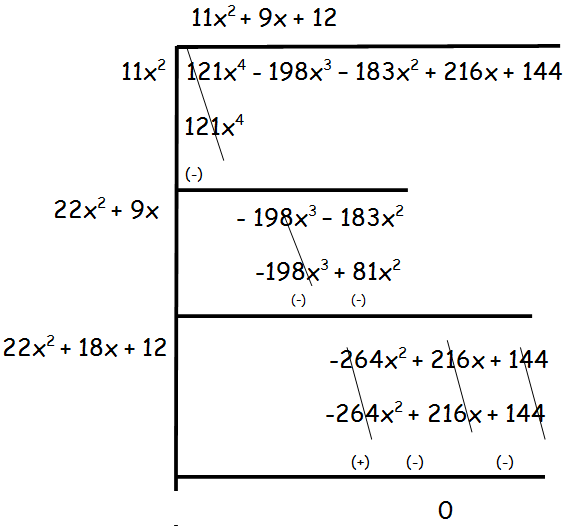
Hence the square root of   121x⁴ − 198x³ − 183x² + 216x + 144 is 11x² + 9x + 12.

Question 2 :

Find the square root of the expression

(x²/y²) - 10x/y + 27 - (10y/x) + (y²/x²)

Solution :

By taking L.C.M, we get

(x⁴ - 10x³y + 27x²y² - 10xy³+ y⁴)/x²y²

=  √(x⁴ - 10x³y + 27x²y² - 10xy³+ y⁴)/√x²y²

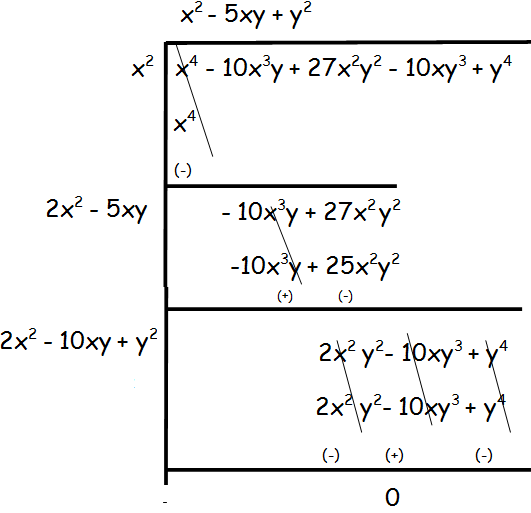
  =  (x² - 5xy + y²)/xy

  =  (x/y)  - 5 + (y/x)

Hence the square root of the polynomial (x²/y²) - 10x/y + 27 - (10y/x) + (y²/x²) is (x/y)  - 5 + (y/x).

Let us look into the next example on "Finding the Square Root of a Polynomial by Long Division Method".

Finding the Missing Value in a Polynomial

Question 1 :

Find the values of a and b if the following polynomials are perfect squares

(i) 4x⁴ −12x³ + 37x² + bx + a

Solution :

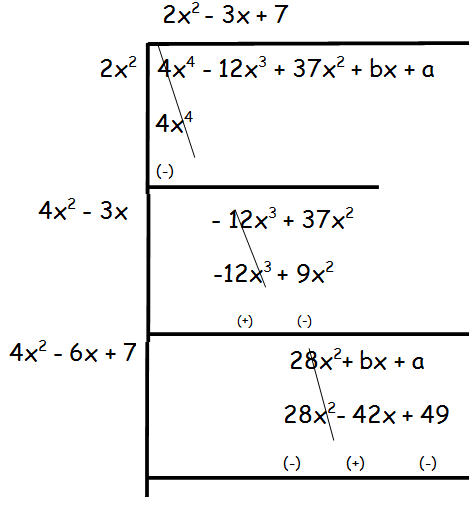
By equating the coefficients of x, we get 

b = -42

By equating the constant terms, we get 

a = 49

Hence the values of a and b are -49 and 42 respectively.

(ii)  ax⁴ + bx³ + 361x² + 220x + 100

Solution :

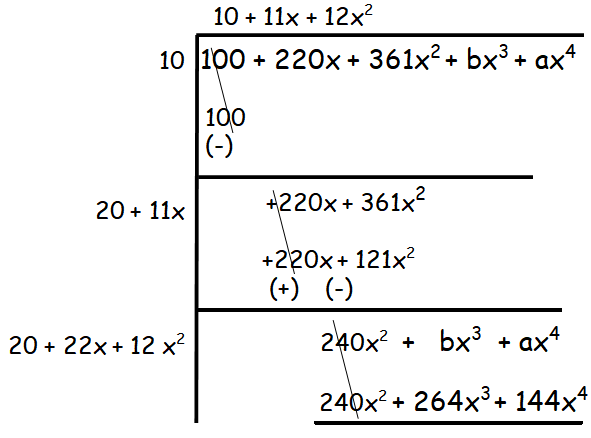
Equating the coefficients of x³, we get 

b  = 264

By equating the coefficients of x⁴, we get 

 a  =  144

Hence the values of a and b are 144 and 264 respectively.

Question 2 :

Find the values of m and n if the following expressions are perfect sqaures

(i)  (1/x⁴) - (6/x³) + (13/x²) + (m/x) + n

Solution :

By taking L.C.M, we get 

(1 - 6x + 13x² + mx³ + nx⁴)/x⁴

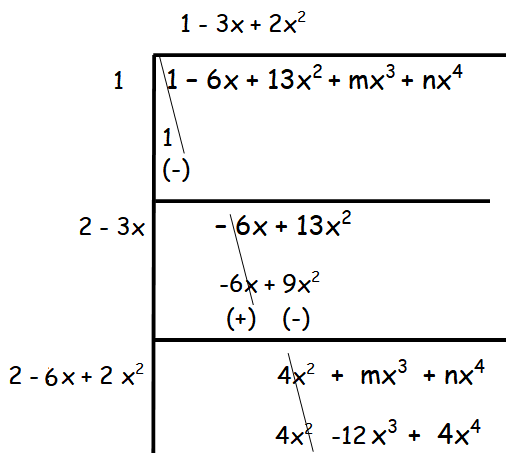
By equating the coefficients of x³, we get 

m = -12

By equating the coefficients of x⁴, we get 

n = 4

Hence the values of m and n are 6 and 4 respectively.

(ii) x⁴ − 8x³ + mx² + nx + 16

Solution :

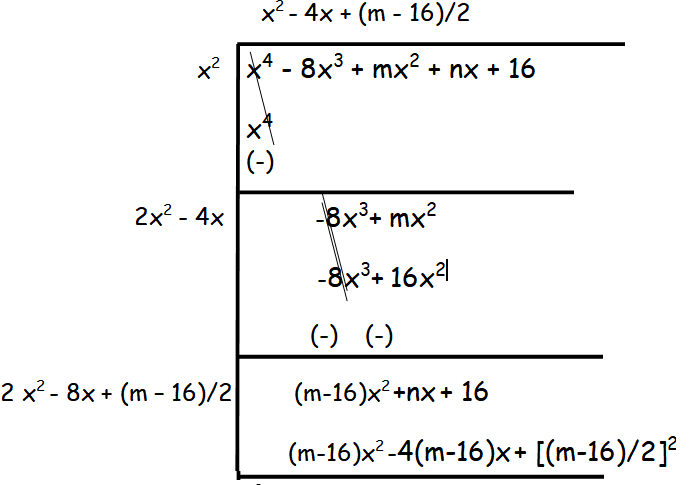
By equating the constant term, we get 

[(m - 16)/2]²  =  16

(m - 16)/2  =  4

m - 16  =  8

m  =  8 + 16  =  24

By equating the coefficients of x, we get

n = -4(m - 16)

n = -4(24 - 16)

n = -4(8)  =  -32

Hence the values of m and n are 24 and -32.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.