FINDING THE VERTEX FOCUS AND DRECTRIX OF A PARABOLA FROM ITS EQUATION

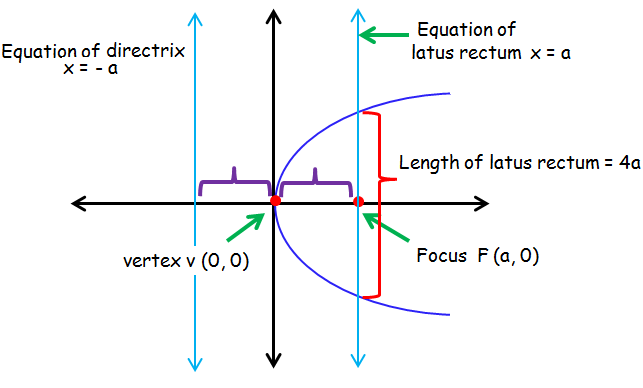
Parabola symmetric about x-axis and open right ward :

Standard form of parabola

y²  =  4ax

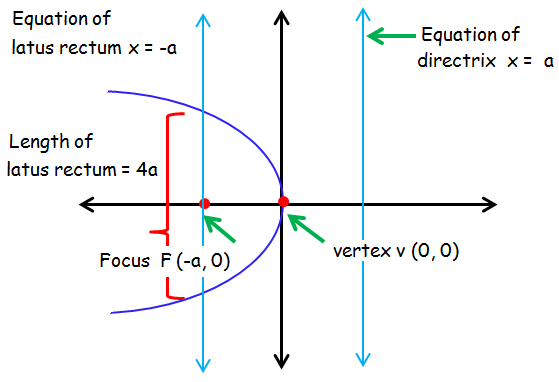
Parabola symmetric about x-axis and open left ward :

Standard form of parabola

y²  =  -4ax

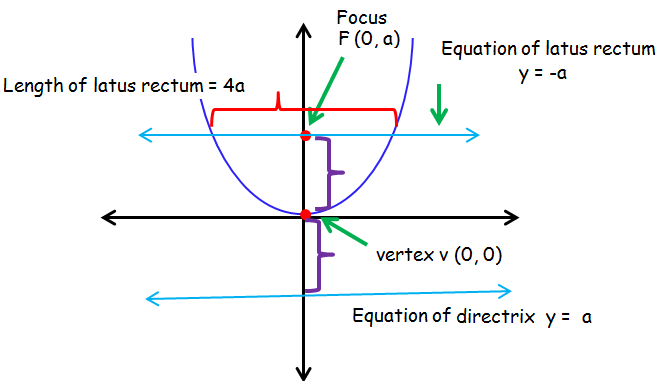
Parabola symmetric about y-axis and open up ward :

Standard form of parabola

x²  =  4ay

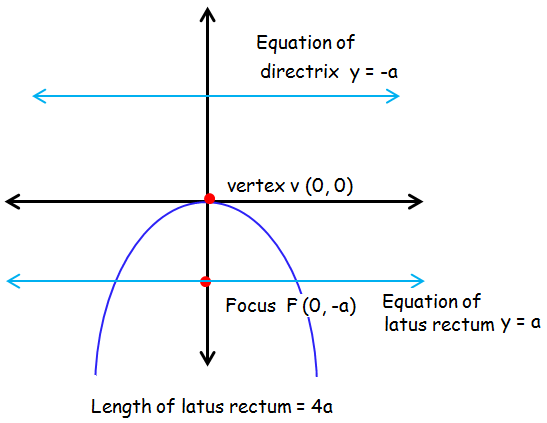
Parabola symmetric about y-axis and open down ward :

Standard form of parabola

x²  =  -4ay

Now let us see some examples based on the above concept.

Example 1 :

Find the focus, vertex, equation of directrix and length of the latus rectum of the parabola

x²  =  5y

Solution :

From the given equation, the parabola is symmetric about y - axis and it is open upward.

x²  =  5y

4a  =  5

a  =  5/4

Vertex : V (0, 0)

Focus : F (0, 5/4)

Equation of directrix : y  =  -5/4

Length of latus rectum :  4a  =  4(5/4)  ==> 5

Example 2 :

Find the focus, vertex, equation of directrix and length of the latus rectum of the parabola

x² - 8y - 2x + 17  =  0

Solution :

x² - 8y - 2x + 17  =  0

x² - 2x  =  8y - 17

x² - 2x + 1² - 1²  =  8y - 17

(x - 1)²  =  8y - 17 + 1

(x - 1)²  =  8y - 16

(x - 1)²  =  8(y - 2)

From the given equation, the parabola is symmetric about y - axis and it is open upward.

Let X  =  x - 1 and Y  =  y - 2

X²  =  8Y

4a  =  8

a  =  2

Example 3 :

Find the focus, vertex, equation of directrix and length of the latus rectum of the parabola

 x²  =  -16y 

Solution :

From the given equation, the parabola is symmetric about y - axis and it is open downward.

x²  =  -16y

4a  =  16

a  =  4

Vertex : V (0, 0)

Focus : F (0, -4)

Equation of directrix : y  =  a  ==>  y  =  4

Length of latus rectum :  4a  =  4(4)  ==> 16

Example 4 :

Find the focus, vertex, equation of directrix and length of the latus rectum of the parabola

x² + 4y - 6x + 17  =  0

Solution :

x² + 4y - 6x + 17  =  0

x² - 6x  =  -4y - 17

x² - 6x + 3² - 3²  =  -4y - 17

(x - 3)²  =  -4y - 17 + 9

(x - 3)²  =  -4y - 8

(x - 3)²  =  -4(y + 2) 

From the given equation, the parabola is symmetric about y - axis and it is open downward.

Let X  =  x - 3 and Y  =  y + 2

X²  =  -4Y

4a  =  4

a  =  1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.