FINDING THE VERTEX OF A PARABOLA PRACTICE PROBLEMS

Write the following quadratics in vertex form  by completing the square and find the vertex.

Problem 1 :

y  =  -x²+2x+3

Solution :

y  =  -x²+2x+3

By factoring negative sign, we get

y  =  -(x²-2x-3)

y  =  -(x²-2⋅x⋅1+1²-1²-3)

y  =  -((x-1)²-4)

y  =  -(x-1)² + 4

By comparing the equation with vertex form of parabola

y  =  a(x-h)² + k

we get the vertex (h, k)  ==>  (1, 4)

Problem 2 :

y  =  2x²+4x-3

Solution :

y  =  2x²+4x-3

By factoring 2, we get

y  =  2(x² + 2x⋅1 + 1² - 1² - (3/2))

y  =  2[(x+1)²-1-(3/2)]

y  =  2[(x+1)²-(5/2)]

By comparing the equation with vertex form of parabola

y  =  a(x-h)² + k

we get the vertex (h, k)  ==>  (-1, -5/2)

Problem 3 :

y  =  -3x²+4x

Solution :

y  =  -3x²+4x

By factoring -3, we get

y  =  -3(x² + (4x/3))

y  =  -3[x² + 2⋅x⋅(2/3) + (2/3)²-(2/3)²]

y  =  -3[x² + 2⋅x⋅(2/3) + (2/3)²-(2/3)²]

y  =  -3[(x+(2/3))²-(2/3)²]

y  =  -3[(x+(2/3))²-(4/9)]

y  =  -3(x+(2/3))²+(4/3)

By comparing the equation with vertex form of parabola

y  =  a(x-h)² + k

we get the vertex (h, k)  ==>  (2/3, 4/3)

Problem 4 :

Suppose you are tossing an apple up to a friend on a third-story balcony. After t seconds, the height of the apple in feet is given by

h  =  –16t² + 38.4t + 0.96

Your friend catches the apple just as it reaches its highest point. How long does the apple take to reach your friend, and at what height above the ground does your friend catch it?

Solution :

The apple travels in parabolic path and it is open downward parabola.

By finding y coordinate in the vertex, we can find the height 

h  =  –16t² + 38.4t + 0.96  --(1)

To find the maximum height of the parabolic path, we find the vertex.

Here a  =  -16, b =  38.4 and c  =  0.96

x-coordinate of vertex  = -b/2a  =  -38.4/2(-16)

t  =  1.2

By applying t  =  1.2 in (1), we get

h  =  –16(1.2)² + 38.4(1.2) + 0.96

h  =  -23.04 + 46.08 + 0.96

h  =  24 feet

So, the required height he caught it is 24 feet.

Problem 5 :

The barber’s profit p each week depends on his charge c per haircut. It is modeled by the equation

p = – 200c²+2400c–4700

What price should he charge for the largest profit?

Solution :

By finding x coordinate of the vertex, we can get the price he should charge for the largest profit.

p  =  – 200c²+2400c–4700

x coordinate  =  -b/2a

Here a  =  -200, b  =  2400 and c  =  -4700

x - coordinate   =  -2400/2(-200)

=  6

To get the largest profit, he should charge $6.

Problem 6 :

A skating rink manager finds that revenue R based on an hourly fee F for skating is represented by the function

R  =  – 480F² + 3120F

What hourly fee will produce maximum revenues?

Solution :

x - coordinate  =  -b/2a

a  =  -480, b  =  3120 and c  =  0

x - coordinate  =  -3120/2(-480)

=  3.25

So, he has to fix hourly fee as $3.25 to produce the maximum revenue.

Problem 7 :

A touch football quarterback passed the ball to a receiver 40 m down field. The path of the ball can be modeled by the following function.

h(d) = -0.01 (d - 20)² + 6

a) What was the maximum height of the ball?

b) What was the horizontal distance of the ball from quarter pack when it reached its maximum height ?

c)  What was he height of the ball when it is thrown ?

d)  If the ball is not caught, what is the distance from quarter pack when the ball lands on the ground.?

Solution :

a)

h(d) = -0.01 (d - 20)² + 6

Comparing the given function with vertex form,

y = a(x - h)² + k

Maximum height is 6 m.

b) The horizontal distance is 20 m.

c)  When the ball is thrown, d = 0

h(d)  = -0.01 (0 - 20)² + 6

= -0.01 (0 - 20)² + 6

= -0.01 (400) + 6

= -4 + 6

= 2

When the ball is thrown the height is 2 m.

d) When the ball lands on ground, the height = 0

0 = -0.01 (d - 20)² + 6

-6 = -0.01 (d - 20)²

6/0.01 = (d - 20)²

(d - 20)² = 600

d - 20 = √600

d - 20 = 24.49

d - 20 = 24.5

d = 24.5 + 20

d = 44.5 m

Problem 8 :

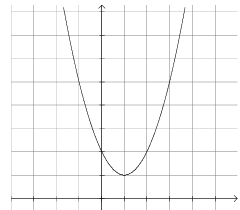
The figure above shows the graph of the quadratic function f has a minimum at the point (1, 1). If f(b) = f(3), which of the following could be the value of b ?

a)  -3    b)  -2     c)  -1     d)  1    e)  5

Solution :

To get the value of f(3), we draw the vertical line at x = 3

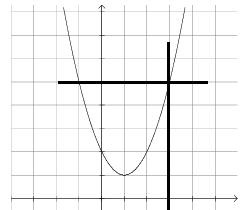
f(3) = 4

f(-1) = 4

So, the value of b is -1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.