FINDING THE VOLUME OF A CYLINDER IN A REAL WORLD CONTEXT

Finding volume of a cylinder is similar to finding volume of a prism.

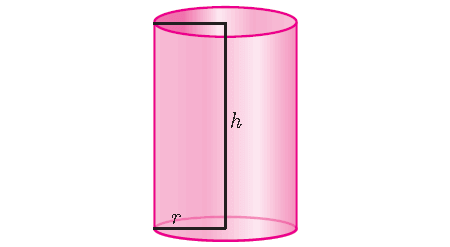
We can find the volume V of both a prism and a cylinder by multiplying the height by the area of the base.

So, the volume of a right circular cylinder of base radius ‘r’ and height ‘h’ is given by

V = (Base Area) x (Height)

The base of a cylinder is a circle, so for a cylinder,

Base Area = πr²

Therefore,

Volume of a cylinder = πr²h cubic units

Example 1 :

The cylindrical Giant Ocean Tank at the New England Aquarium in Boston is 24 feet deep and has a radius of 18.8 feet. Find the volume of the tank. Use the approximate of value of  ∏, that is 3.14 and round your answer to the nearest tenth if necessary.

Solution :

Step 1 : 

Because the tank is in the shape of cylinder, we can use the formula of volume of a cylinder to find volume of the tank.

V = πr²h cubic units

Step 2 : 

Substitute the given measures. 

V ≈ 3.14 · 18.8² · 24

(Here deep 24 feet is considered as height)

Simplify.

V ≈ 3.14 · 353.44 · 24

V ≈ 26635.2

So, the volume of the tank is about 26635.2 cubic feet.

Example 2 :

A standard-size bass drum has a diameter of 22 inches  and is 18 inches deep. Find the volume of this drum. Use the approximate of value of  ∏, that is 3.14 and round your answer to the nearest tenth if necessary.

Solution :

Step 1 : 

Usually the bass drum would be in the shape of cylinder. So, we can use the formula of volume of a cylinder, to find volume of the bass drum.

V = πr²h cubic units -----(1)

Step 2 : 

To find the volume, we need the radius of the cylinder. But, the diameter is given, that is 22 in. So, find the radius. 

r = diameter/2

r = 22/2

r = 11

Step 3 :

Substitute π ≈  3.14, r = 11 and h = 18 in (1).

V ≈ 3.14 · 11² · 18

(Here deep 18 inches is considered as height)

Simplify.

V ≈ 3.14 · 121 · 18

V ≈ 6838.9

So, the volume of the bass drum is about 6838.9 cubic inches.

Example 3 :

A barrel of crude oil contains about 5.61 cubic feet of oil. How many barrels of oil are contained in 1 mile of a pipeline that has an inside diameter of 6 inches and is completely filled with oil ? How much is “1 mile” of oil in this pipeline worth at a price of $100 per barrel ?

Solution :

Step 1 : 

Usually the pipe line would be in the shape of cylinder. So, we can use the formula of volume of a cylinder to find volume of the crude oil in the pipe line. 

V = πr²h cubic units -----(1)

Step 2 : 

To find the volume, we need the radius of the cylinder. But, the diameter is given, that is 6 in. So, find the radius. 

r = diameter/2

r = 6/2

r = 3 inches

Step 3 :

Convert the inches into feet by multiplying 1/12.

Because, 

1 inch = 1/12 feet

So, we have 

r = 3 x 1/12 feet

r = 1/4 feet

Step 4 :

Convert the length of the pipeline from miles to feet.

1 mile = 5280 feet

So, we have 

length = 1 mile

length = 1 x 5280 feet

length = 5280 feet

Step 5 :

Substitute π  ≈  3.14, r = 1/4 and h = 5280 in (1).

V ≈ 3.14 · (1/4)² · 5280

(Here , the length 5280 feet is considered as height)

Simplify.

V ≈ 3.14 · (1/16) · 5280

V ≈ 1036.2 cubic feet

Step 6 :

To find how many barrels of oil are contained in 1 mile of a pipeline, divide the volume of crude oil in the pipeline (1036.2 cu.ft) by 5.61.

Because a barrel of crude oil contains about 5.61 cubic feet of oil.

So, number of barrels of oil are contained in 1 mile of a pipeline is 

= 1036.2 / 5.61

= 184.7

There are about 184.7 barrels of oil are contained in 1 mile of a pipeline.

Step 7 :

Find the worth of “1 mile” of oil in the pipeline at a price of $100 per barrel.

No. of barrels of oil in 1 mile of a pipeline  =  184.7  

So, the worth of “1 mile” of oil in the pipeline is 

= $100 x 184.7

= $18,470

The worth of “1 mile” of oil in the pipeline at a price of $100 per barrel is about $18,470.

Example 4 :

A pan for baking French bread is shaped like half a cylinder as shown in the figure. Find the volume of uncooked dough that would fill this pan. Use the approximate of value of  ∏, that is 3.14 and round your answer to the nearest tenth if necessary.

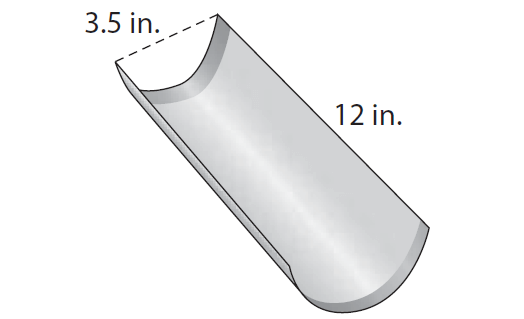
Solution :

Step 1 : 

Because the pan is shaped like half a cylinder, we can use the formula of volume of a cylinder to find volume of uncooked dough that would fill this pan

V = 1/2 · πr²h cubic units -----(1)

(Because the pan is shaped like half a cylinder, 1/2 is multiplied by the formula of volume of a cylinder)

Step 2 : 

To find the volume, we need the radius of the cylinder. But, the diameter is given, that is 3.5 in. So, find the radius. 

r = diameter/2

r = 3.5/2

r = 1.75

Step 3 :

Substitute π ≈ 3.14, r = 1.75 and h = 12 in (1).

V ≈ 1/2 · 3.14 · 1.75² · 12

Simplify.

V ≈ 1/2 · 3.14 · 3.0625 · 12

V ≈ 57.7

So, the volume of uncooked dough that would fill the pan is about 57.7 cu.inches.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.