FINDING THE VOLUME OF A SPHERE

We can find the volume of a sphere using the volume of a cylinder. 

Cylinder is a solid which has a circular base. 

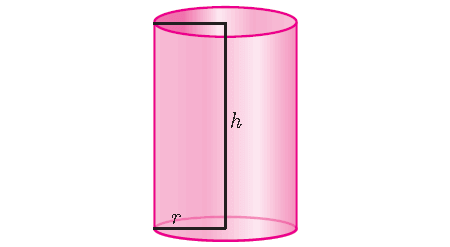
We know the fact that the volume of any solid is equal to the product of base area and height of the solid.

So, the volume of a right circular cylinder of base radius ‘r’ and height ‘h’ is given by

V = (Base Area) x (Height) 

The base of a cylinder is a circle, so for a cylinder,

Base Area = πr²

Therefore, 

Volume of a cylinder = πr²h cubic units

Consider a right circular cylinder and three right circular cones of same base radius and height as that of the cylinder.

The contents of three cones will exactly occupy the cylinder.

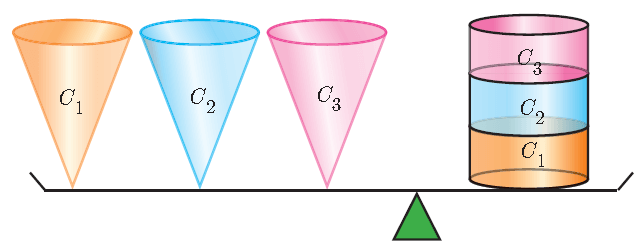
Then,

When we model the volume of a sphere, we will be getting the following result. 

3 x (Volume of a cone) = Volume of cylinder

3 x (Volume of a cone) = πr²h

Volume of the cone = 1/3 · πr²h cubic units

Consider a sphere and two right circular cones of same base radius and height such that twice the radius of the sphere is equal to the height of the cones.

Then we can observe that the contents of two cones will exactly occupy the sphere.

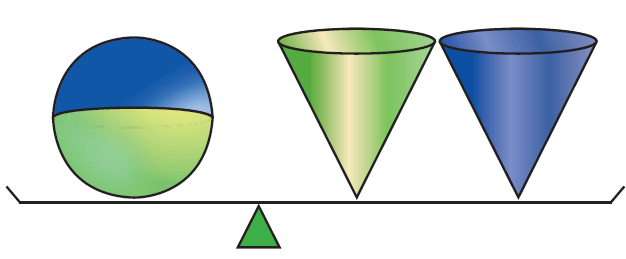
Then, 

Volume of sphere = 2 x (Volume of a cone)

Volume of a sphere = 2 x (1/3 · πr²h)

Volume of a sphere = 2/3 · πr²h

A sphere always has a height which is equal to twice the radius.

So, substitute 2r for h.

Volume of sphere = 2/3 · πr²(2r)

Simplify.

Volume of sphere = 4/3 · πr³ cubic units

Example 1 :

Find the volume of the sphere given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14. 

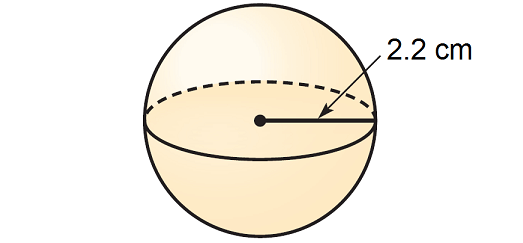
Solution :

Step 1 : 

Write the formula to find volume of a sphere.

V = 4/3 ·  πr³

Step 2 : 

Substitute the given measures. 

V ≈ 4/3 · 3.14 · (2.2)³

Simplify.

V ≈ 4/3 · 3.14 · 10.648

V ≈ 44.6

So, the volume of the given sphere is about 44.6 cubic cm.

Example 2 :

Find the volume of the sphere given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14. 

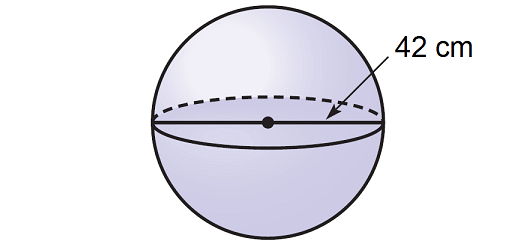
Solution :

Step 1 :

Write the formula to find volume of a sphere.

V = 4/3 ·  πr³ -----(1)

Step 2 :

To find the volume, we need the radius of the sphere. But, the diameter is given, that is  42 cm. So, find the radius.

r = diameter/2

r = 42/2

r = 21

Step 3 :

Substitute π ≈ 3.14 and r = 21 in (1).

V ≈ 4/3 · 3.14 · 21³

Simplify.

V ≈ 4/3 · 3.14 · 9261

V ≈ 38,772.7

So, the volume of the given sphere is about 38,772.7 cubic cm.

Example 3 :

Find the volume of the sphere given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14.

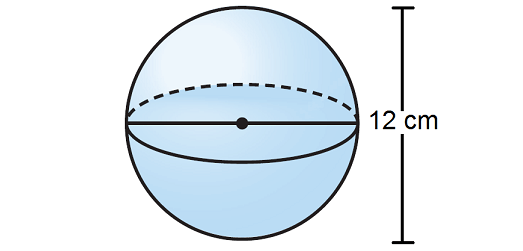
Solution :

Step 1 :

Write the formula to find volume of a sphere.

V = 4/3 ·  πr³ -----(1)

Step 2 :

To find the volume, we need the radius of the sphere. But, the height is given, that is  12 cm.

We know that the height of a sphere equals twice the radius.

That is,

h = 2r

Substitute h = 12.

12 = 2r

Divide both sides by 2.

12/2 = 2r/2

6 = r

Step 3 :

Substitute π ≈ 3.14 and r = 6 in (1).

V ≈ 4/3 · 3.14 · 6³

Simplify.

V ≈ 4/3 · 3.14 · 216

V ≈ 904.3

So, the volume of the given sphere is about 904.3 cubic cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.