FINDING THE X INTERCEPTS OF A QUADRATIC FUNCTION
The graph of a quadratic function is a parabola. When a parabola opens up/down, we may have a chance to have x-intercepts.
x-intercepts are the numbers on the x-axis where a parabola intersects x-axis.
Sometimes a parabola may not intersect x-axis. In that case, there are are no x-intercepts.
Consider the quadratic function given below.
y = ax2 + bx + c
Substitute f(x) = 0 in the above quadratic function to find x-intercepts.
0 = ax2 + bx + c
or
ax2 + bx + c = 0
The above is a quadratic equation and it is also called standard form of quadratic equation.
When we solve a quadratic equation, we have a chance to get two values for x. Because the degree (largest exponent) of the equation is 2.
Those two values of x are called x-intercepts.
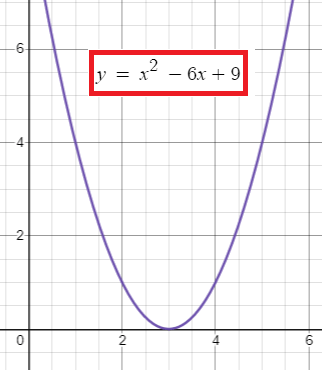
Quadratic Function with One X-Intercept
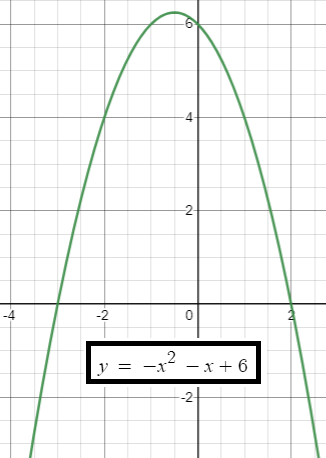
Quadratic Function with Two X-Intercepts
Find the x intercept(s) of the quadratic functions :
Example 1 :
y = x2- 6x + 9
Solution :
y = x2 - 6x + 9
Substitute y = 0 to to find x-intercepts.
x2 - 6x + 9 = 0
In the quadratic equation above, the coefficient of x2 is 1. So, get two factors of the constant term '+9' such that the sum of the two factors is equal to the coefficient of x, that is '-6'.
Then the two factors of '+9' are '-3' and '-3'.
Now, split the middle term -6x using the two factors -3 and -3.
x2 - 6x + 9 = 0
x2 - 3x - 3x + 9 = 0
x(x - 3) - 3(x - 3) = 0
(x - 3)(x - 3) = 0
(x - 3)2 = 0
Taking square root on both sides,
x - 3 = 0
x = 3
The given quadratic expression has only one x-intercept and it is 3.
Example 2 :
y = x2 - 3x + 2
Solution :
y = x2 - 3x + 2
Substitute y = 0 to to find x-intercepts.
x2 - 3x + 2 = 0
In the quadratic equation above, the coefficient of x2 is 1. So, get two factors of the constant term '+2' such that the sum of the two factors is equal to the coefficient of x, that is '-3'.
Then the two factors of '+2' are '-1' and '-2'.
Now, split the middle term -3x using the two factors -1 and -2.
x2 - 3x + 2 = 0
x2 - 1x - 2x + 2 = 0
x(x - 1) - 2(x - 1) = 0
(x - 1)(x - 2) = 0
x - 1 = 0 or x - 2 = 0
x = 1 or x = 2
The given quadratic expression has two x-intercepts and they are 1 and 2.
Example 3 :
y = -9x2 + 4
Solution :
Substitute y = 0 to to find x-intercepts.
-9x2 + 4 = 0
Multiply both sides by -1.
9x2 - 4 = 0
32x2 - 4 = 0
(3x)2 - 22 = 0
Using the identity a2 - b2 = (a + b)(a - b),
(3x + 2)(3x - 2) = 0
3x + 2 = 0 or 3x - 2 = 0
x = -2/3 or x = 2/3
The given quadratic expression has two x-intercepts and they are -2/3 and 2/3.
Example 4 :
y = 3x2 - x - 2
Solution :
Substitute y = 0 to to find x-intercepts.
3x2 - x - 2 = 0
In the quadratic expression above, the coefficient of x2 is 3.
Multiply the coefficient of x2 and the constant term -2.
3x(-2) = -6
Now, get two factors of '-6' such that the sum of the two factors is equal to the coefficient of x, that is '-1'.
Then the two factors of '-6' are '+2' and '-3'.
Now, split the middle term -x using the two factors +2 and -3.
3x2 - x - 2 = 0
3x2 + 2x - 3x - 2 = 0
x(3x + 2) - 1(3x + 2) = 0
(3x + 2)(x - 1) = 0
3x + 2 = 0 or x - 1 = 0
x = -2/3 and x = 1
The given quadratic function has two x-intercept and they are -2/3 and 1.
Example 5 :
y = -(x - 1)(x - 3)
Solution :
y = -(x - 1)(x - 3)
Substitute y = 0 to to find x-intercepts.
-(x - 1)(x - 3) = 0
Multiply both sides of the equation by -1.
(x - 1)(x - 3) = 0
x - 1 = 0 or x - 3 = 0
x = 1 or x = 3
The given quadratic function has two x-intercept and they are 1 and 3.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)

