FINDING UNKNOWN ANGLE MEASURES WORKSHEET
Problem 1 :
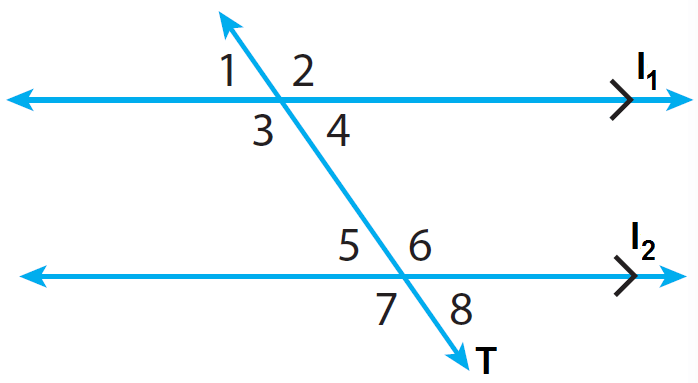
In the diagram given below, the lines l1 and l2 are parallel and the line T is transversal. Find m∠2 when m∠7 = 120°.
Problem 2 :
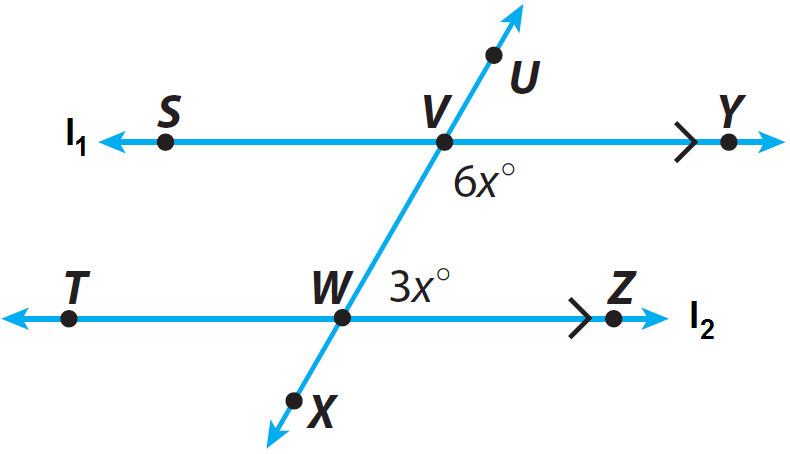
In the diagram given below, the lines l1 and l2 are parallel and the line T is transversal. Find m∠VWZ.
Problem 3 :
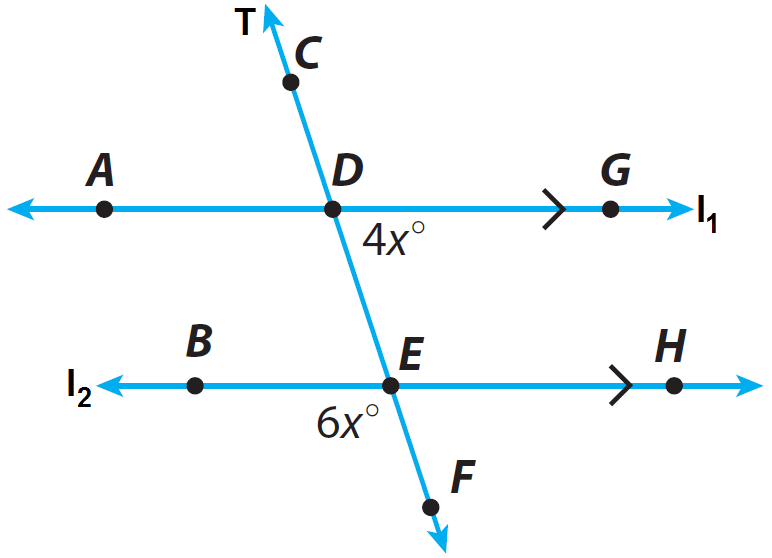
In the diagram given below, the lines l1 and l2 are parallel and the line T is transversal. Find m∠GDE.
Problem 4 :
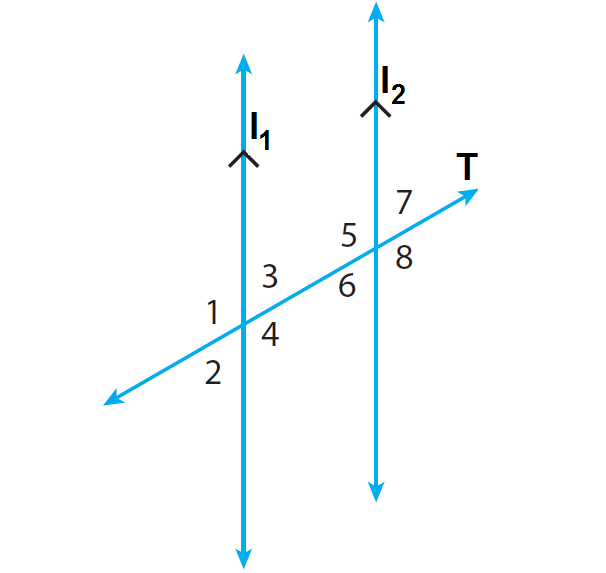
In the diagram given below, the lines l1 and l2 are parallel and the line T is transversal. Find m∠3 when m∠7 = 65°.

Answers
1. Answer :

Step 1 :
In the above diagram, m∠2 and m∠7 are alternate interior angles.
Step 2 :
When two parallel lines are cut by a transversal, alternate interior angles are congruent.
So, we have
m∠2 = m∠7
m∠2 = 120°
2. Answer :

Step 1 :
In the above diagram, m∠VWZ and m∠YVW are same-side interior angles.
Step 2 :
When two parallel lines are cut by a transversal, same-side interior angles are supplementary.
So, we have
m∠VWZ + m∠YVW = 180°
Step 3 :
From the diagram given above, we have m∠VWZ = 3x and m∠YVW = 6x. So, replace m∠VWZ by 3x and m∠YVW by 6x.
3x° + 6x° = 180°
Combine like terms.
9x° = 180°
Divide both sides by 9.
x° = 20°
Step 4 :
Substitute x = 20° into m∠VWZ = 3x°.
m∠VWZ = 3 · 20°
m∠VWZ = 60°
3. Answer :

Step 1 :
In the above diagram, m∠GDE and m∠ADE are angles on the straight line l₁.
So, we have
m∠GDE + m∠ADE = 180° -----(1)
Step 2 :
In the above diagram, m∠ADE and m∠BEF are corresponding angles and corresponding angles are always congruent.
So, we have
m∠ADE = m∠BEF
Step 3 :
In (1) replace m∠ADE by m∠BEF
(1) -----> m∠GDE + m∠BEF = 180°
Step 4 :
From the diagram given above, we have m∠GDE = 4x and m∠BEF = 6x. So, replace m∠GDE by 4x and m∠BEF by 6x.
4x° + 6x° = 180°
Combine like terms.
10x° = 180°
x° = 18°
Step 5 :
Substitute x° = 18° into m∠GDE = 4x°.
m∠GDE = 4 · 18°
m∠GDE = 72°
4. Answer :

Step 1 :
In the above diagram, m∠6 and m∠7 are vertially opposite angles and they are congruent.
m∠6 = m∠7
m∠6 = 65°
Step 2 :
In the above diagram, m∠3 and m∠6 are alternate interior angles and they are congruent.
m∠3 = m∠6
m∠3 = 65°
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 134)
Apr 02, 25 12:40 AM
Digital SAT Math Problems and Solutions (Part - 134) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Apr 02, 25 12:35 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part 135)
Apr 02, 25 12:32 AM
Digital SAT Math Problems and Solutions (Part 135)