FREE ONLINE GRADE 9 MATH PRACTICE

Problem 1 :

If two lines intersect, then the vertically opposite angles are

 (A) Equal            (B) Perpendicular           (C) Not to equal

Solution :

If two lines are intersecting then the vertically opposite angles are equal.

Problem 2 :

If a side of a triangle is produced, so the exterior angle so formed is equal to the sum of the interior opposite angles. The above statement is

 (A) False             (B) True          (C) Neither

Problem 3 :

Find the sum of the digits of square of following number

111 111 111

Solution :

To find the square of the given number which is containing 9 one's, let us find the pattern.

11 x 11  =  121

111 x 111  =  12321

1111 x 1111 =  1234321

11111 x 11111  =  123454321

...................

111 111 111 x 111 111 111  =  12345678987654321

In this answer, 1, 2, 3, 4, ,5, 6, 7, 8 are repeating twice and 9 is appearing once.

  =  2[1+2+3+4+5+6+7+8] + 9

  =  2(36) + 9

  =  72+9

  =  81

Problem 4 :

What is the value of x in the below figure ?

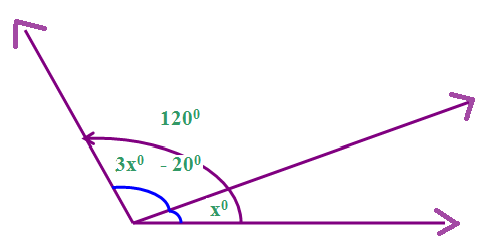
Solution :

Sum of the above anges is 120

3x -20 + x  =  120

4x-20  =  120

4x  =  140

x  =  140/4

x  =  35

Problem 5 :

Find the value of x and y in the following figure ?

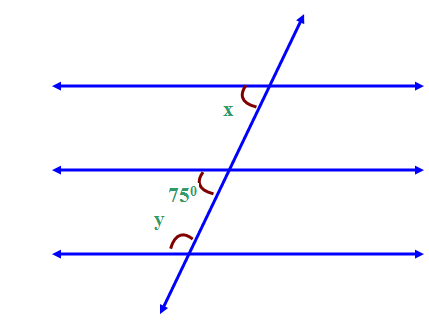
Solution :

x  =  75

Sum of interior angle is 180.

y + 75  =  180

y  =  180-75

y  =  105

Problem 6 :

In the year , the United States will host the  International Mathematical Olympiad Let I, M and O be distinct positive integers such that the product I ⋅ M ⋅ O  =  2001. What is the largest possible value of the sum I + M + O ?

(A)  23          (B)  671         (C)   1008

Solution :

 I ⋅ M ⋅ O  =  2001

By finding prime factors of 2001, we get 

 I ⋅ M ⋅ O  =  3 ⋅ 667 ⋅ 1

I + M + O  =  3 + 667 + 1

  =  671

Problem 7 :

Find the smaller and larger angles in the following figure

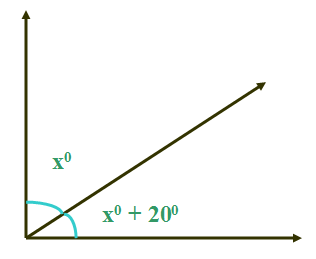
Solution :

x + x + 20  =  70

2x + 20  =  70

3x  =  50

x  =  25

Problem 8 :

Each day, Jenny ate 20% of the jellybeans that were in her jar at the beginning of that day. At the end of the second day, 32 remained. How many jellybeans were in the jar originally?

(a)  40                 (B)  50             (C)  60

Solution :

Let x be the quantity of jelly beans in the jar.

20% of x + 20% of 80x + 32  =  x

0.2x + 0.16x + 32  =  x

32  =  x - 0.36x

32  =  0.64x

x  =  32/0.64

x  =  50

So, the original number o jelly beans is 50.

Problem 9 :

Chandra pays an on-line service provider a fixed monthly fee plus an hourly charge for connect time. Her December bill was $12.48, but in January her bill was $17.54  because she used twice as much connect time as in December. What is the fixed monthly fee?

(A)  $5.06           (B)  $6.24        (C)  $7.42

Solution :

Let x be fixed charge and y be the hourly charge.

x + y =  12.48  (December)  ---(1)

x + 2y =  17.54  (January) ---(2)

(1) - (2)

-y  =  -5.06

y  =  5.06

By applying the value of y in (1), we get

x + 5.06  =  12.48

x  =  7.42

So, her monthly fixed fee is $7.42.

Problem 10 :

Find the slope of the line passing through

(5, 6) and (15, 9)

Solution :

Slope  =  (y₂ - y₁)/(x₂-x₁)

  =  (9-6)/(15-5)

  =  3/10

So, the slope of the line joining the above points is 3/10.

Answer Key

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.