FRIEZE PATTERNS GEOMETRY

A frieze pattern or border pattern is a pattern that extends to the left and right in such a way that the pattern can be mapped onto itself by a horizontal translation. In addition to being mapped onto itself by a horizontal translation, some frieze patterns can be mapped onto themselves by other transformations.

1.  Translations                                    T

2.  180° rotation                                  R

3.  Reflection in a horizontal line         H

4.  Reflection in a vertical line             V

5.  Horizontal glide reflection             G

Describing Frieze Patterns

Example 1 :

Describe the transformations that will map each frieze pattern onto itself.

Solution :

a. This frieze pattern can be mapped onto itself by a horizontal translation (T).

b. This frieze pattern can be mapped onto itself by a horizontal translation (T) or by a 180° rotation (R).

c. This frieze pattern can be mapped onto itself by a horizontal translation (T) or by a horizontal glide reflection (G).

d. This frieze pattern can be mapped onto itself by a horizontal translation (T) or by a reflection in a vertical line (V).

Classifications of Frieze Patterns

T - Translation :

TR - Translation and 180° rotation :

TG - Translation and horizontal glide reflection :

TV - Translation and vertical glide reflection :

THG - Translation, horizontal line reflection and vertical glide reflection :

TRVG - Translation, 180° rotation, vertical line reflection and horizontal glide reflection :

TRHVG - Translation, 180° rotation, horizontal line reflection, vertical line reflection and horizontal glide reflection :

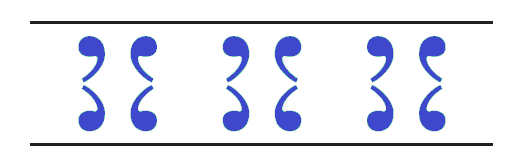
To classify a frieze pattern into one of the seven categories, first decide whether the pattern has 180° rotation. If it does, then there are three possible classifications: TR, TRVG, and TRHVG.

If the frieze pattern does not have 180° rotation, then there are four possible classifications: T, TV, TG, and THG. Decide whether the pattern has a line of reflection. By a process of elimination, you will reach the correct classification.

Classifying a Frieze Pattern 

Example 2 :

Categorize the snakeskin pattern of the mountain adder.

Solution :

This pattern is a TRHVG. The pattern can be mapped onto itself by a translation, a 180° rotation, a reflection in a horizontal line, a reflection in a vertical line, and a horizontal glide reflection.

Using Frieze Patterns in Real Life

Example (Identifying Frieze Patterns) :

The frieze patterns of ancient Doric buildings are located between the cornice and the architrave, as shown below.

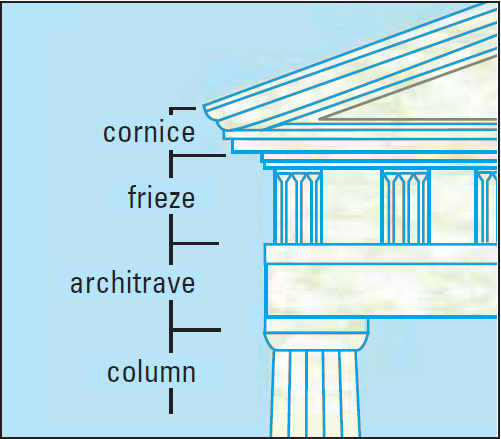
The frieze patterns consist of alternating sections. Some sections contain a person or a symmetric design. Other sections have simple patterns of three or four vertical lines.

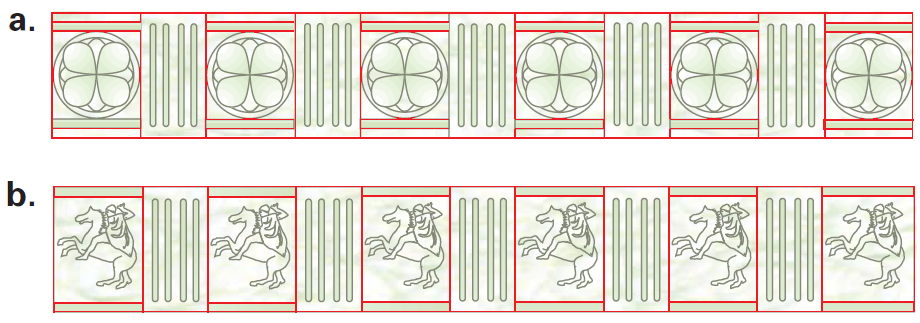
Portions of two frieze patterns are shown below. Classify the patterns.

Solution :

a. Following the diagrams on the previous page, you can see that this frieze pattern has rotational symmetry, line symmetry about a horizontal line and a vertical line, and that the pattern can be mapped onto itself by a glide reflection. So, the pattern can be classified as TRHVG.

b. The only transformation that maps this pattern onto itself is a translation. So, the pattern can be classified as T.

Drawing a Frieze Pattern

Example 3 :

A border on a bathroom wall is created using the decorative tile at the right. The border pattern is classified as TR. Draw one such pattern.

Solution :

Begin by rotating the given tile 180°. Use this tile and the original tile to create a pattern that has rotational symmetry. Then translate the pattern several times to create the frieze pattern.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.