FRIEZE PATTERNS WORKSHEET

Problem 1 :

Describe the transformations that will map each frieze pattern onto itself.

Problem 2 :

Categorize the snakeskin pattern of the mountain adder.

Problem 3 :

The frieze patterns of ancient Doric buildings are located between the cornice and the architrave, as shown below.

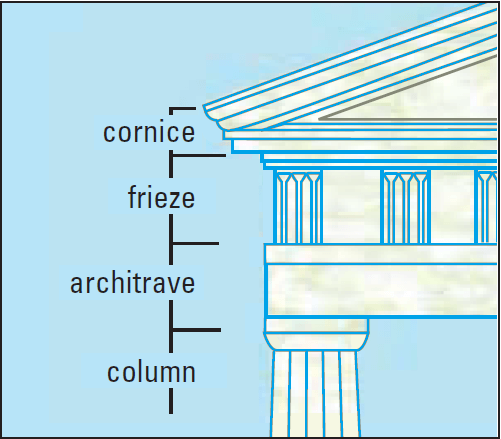
The frieze patterns consist of alternating sections. Some sections contain a person or a symmetric design. Other sections have simple patterns of three or four vertical lines. 

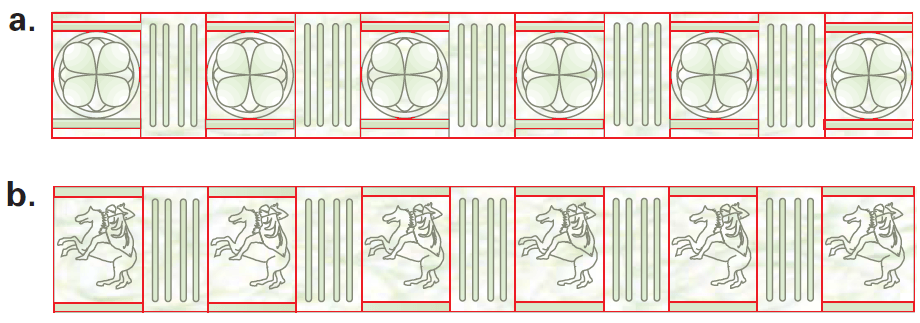
Portions of two frieze patterns are shown below. Classify the patterns.

Problem 4 :

A border on a bathroom wall is created using the decorative tile shown below. The border pattern is classified as TR. Draw one such pattern.

1. Answer :

a. This frieze pattern can be mapped onto itself by a horizontal translation (T).

b. This frieze pattern can be mapped onto itself by a horizontal translation (T) or by a 180° rotation (R).

c. This frieze pattern can be mapped onto itself by a horizontal translation (T) or by a horizontal glide reflection (G).

d. This frieze pattern can be mapped onto itself by a horizontal translation (T) or by a reflection in a vertical line (V).

2. Answer :

This pattern is a TRHVG. The pattern can be mapped onto itself by a translation, a 180° rotation, a reflection in a horizontal line, a reflection in a vertical line, and a horizontal glide reflection.

3. Answer :

The frieze patterns consist of alternating sections. Some sections contain a person or a symmetric design. Other sections have simple patterns of three or four vertical lines. 

Portions of two frieze patterns are shown below. Classify the patterns.

a. Following the diagrams on the previous page, you can see that this frieze pattern has rotational symmetry, line symmetry about a horizontal line and a vertical line, and that the pattern can be mapped onto itself by a glide reflection. So, the pattern can be classified as TRHVG.

b. The only transformation that maps this pattern onto itself is a translation. So, the pattern can be classified as T.

4. Answer :

Begin by rotating the given tile 180°. Use this tile and the original tile to create a pattern that has rotational symmetry. Then translate the pattern several times to create the frieze pattern.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.