FUNDAMENTAL COUNTING PRINCIPLE WORKSHEET WITH ANSWERS

Question 1 :

In a class there are 27 boys and 14 girls. The teacher wants to select 1 boy and 1 girl to represent a competition. In how many ways can the teacher make this selection ?

Question 2 :

Given 7 flags of different colors, how many different signals can be generated if a signal requires the use of two flags, one below the other ?

Question 3 :

A person wants to buy one fountain pen, one ball pen and one pencil from a stationery shop. If there are 10 fountain pen varieties, 12 ball pen varieties and 5 pencil varieties, in how many ways can he select these articles ?

Question 4:

Twelve students compete in a race. In how many ways first three prizes be given ?

Question 5 :

From among the 36 teachers in a college, one principal, one vice-principal and the teacher-in charge are to be appointed. In how many ways this can be done ?

Question 6 :

There are 6 multiple choice questions in an examination. How many sequences of answers are possible, if the first three questions have 4 choices each and the next three have 2 each ?

Question 7 :

How many numbers are there between 500 and 1000 which have exactly one of their digits as 8 ?

Question 8 : 

How many five-digit number license plates can be made if 

(i) first digit cannot be zero and the repetition of digits is not allowed.

(ii) the first digit cannot be zero, but the repetition of digits is allowed ?

Detailed Answer Key

Question 1 :

In a class there are 27 boys and 14 girls. The teacher wants to select 1 boy and 1 girl to represent a competition. In how many ways can the teacher make this selection ?

Answer :

Number of ways of selecting a boy  =  27

Number of ways of selecting a girl  =  14

From the given question, we come to know that we can select a boy or a girl. That is, it is enough to do one of the works. 

So, we have to use the concept principle of addition.

Total number of ways to make this selection  =  27 + 14

  =  41 ways

So, the teacher can make this selection is 41 ways.

Question 2 :

Given 7 flags of different colors, how many different signals can be generated if a signal requires the use of two flags, one below the other?

Answer :

We have to choose two flags,

Number of ways of selecting 1st flag  =  7

After selecting the first flag, we cannot choose the same color flag again.

Number of ways of selecting 2nd flag  =  6

Since we have to choose two flags, we have to multiply 7 and 6.

  =  7 x 6  =  42

So, the number of ways of selecting two flags is 42.

Question 3 :

A person wants to buy one fountain pen, one ball pen and one pencil from a stationery shop. If there are 10 fountain pen varieties, 12 ball pen varieties and 5 pencil varieties, in how many ways can he select these articles?

Answer :

A person need to buy fountain pen, one ball pen and one pencil. That is we have to do all the works

Number of ways selecting fountain pen  =  10

Number of ways selecting ball pen  =  12

Number of ways selecting pencil  =  5

Total number of selecting all these  =  10 x 12 x 5

  =  600

Question 4:

Twelve students compete in a race. In how many ways first three prizes be given?

Answer :

Total number of students  =  12

All the students will have equal chance to get 1st prize

Number of ways to get the first prize  =  12

Out of 12 students, only 11 students are eligible to get the second prize. Because 1 student got the first prize already. 

Number of ways to get the second prize  =  11

Out of 12 students, only 10 students are eligible to get the second prize. Because for the 2 students already got  the first and second prize respectively.

Number of ways to get the third prize  =  10

Total number of ways  =  12 x 11 x 10  =  1320

Question 5 :

From among the 36 teachers in a college, one principal, one vice-principal and the teacher-in charge are to be appointed. In how many ways this can be done?

Answer :

Total number of teachers  =  36

So, the total number of ways  =  36 x 35 x 34

  =  42840

Question 6 :

There are 6 multiple choice questions in an examination. How many sequences of answers are possible, if the first three questions have 4 choices each and the next three have 2 each ?

Answer :

We have to answer for all 6 questions.

  _____ x ______ x ______  x ______ x ______ x ______ 

To answer the first question, we have 4 ways.

To answer the second question, we have 4 ways.

To answer the third question, we have 4 ways.

To answer the fourth question, we have 2 ways.

To answer the fifth question, we have 2 ways.

To answer the sixth question, we have 2 ways.

=   4  x  4  x 4  x  2  x  2  x  2

=  512

So, the total number ways to answer 6 questions is 512.

Question 7 :

How many numbers are there between 500 and 1000 which have exactly one of their digits as 8?

Answer :

The unit digit of the number lies between 500 and 1000 are 5, 6, 7, 8, 9. By using one of the numbers in the unit digit, we can get three digit numbers.

Now the condition is one of their digits as 8. 

(i) If the hundred's digit is 8, then the other two digits may be any number.

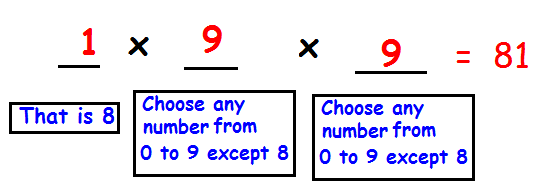
(ii) If the ten's digit is 8, then the other two digits may be any number.

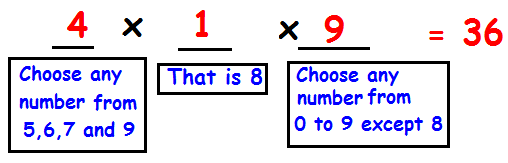
(iii) If the one's digit is 8, then the other two digits may be any number.

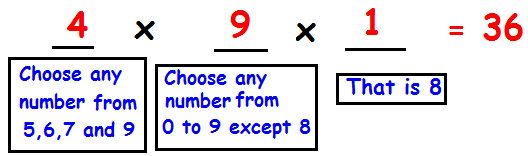
Total number of ways  =  81 + 36 + 36

   =   153

Question 8 : 

How many five-digit number license plates can be made if 

(i) first digit cannot be zero and the repetition of digits is not allowed.

(ii) the first digit cannot be zero, but the repetition of digits is allowed?

Answer :

Numbers can be filled in the places are 0,1,2,3,4,........9

___ x ____ x ____ x ____ x ____

Number of options we have for first place  =  9 (except 0)

Since repetition is not allowed the second dash is having 9 options (including 0 except the number filled in the first dash).

Like wise the third, fourth and fifth dashes are having 8, 7 and 6 options respectively.

Total number of ways  =  9 x 9 x 8 x 7 x 6

  =  27216

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.