GENERAL AND MIDDLE TERMS OF BINOMIAL EXPANSION

Here we are going to see how to find the middle term in binomial expansion.

General term :

T_(r+1) =  ⁿc_r x^(n-r) a^r

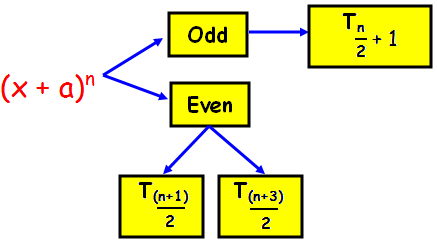
The number of terms in the expansion of (x + a)ⁿ depends upon the index n. The index is either even (or) odd.

Let us find the middle terms.

Case (i) : n is even 

The number of terms in the expansion is (n + 1), which is odd. Hence, there is only one middle term and it is given by T_{(n/2) + 1}

Case (ii) : n is odd

The number of terms in the expansion is (n + 1), which is even. Hence, there are two middle terms and they are given by T_{(n + 1)/2} and T_{(n + 3)/2}

Example 1 :

Find the constant term in the expansion (√x - 2/x²)¹⁰

Solution :

T_(r+1) =  ⁿc_r x^(n-r) a^r

Comparing the given expression with the form (x + a)ⁿ, we get x = √x, a = -2/x² and n = 10

T_(r+1) =  ¹⁰c_r √x^(10-r) (-2/x²)^r

=  ¹⁰c_r x^1/2(10-r) (-2x^-2)^r

=  ¹⁰c_r x^(10-r)/2 (-2x^-2)^r

= (-2)^r 10c_r x^(10-r)/2 x^-2r

= (-2)^r 10c_r x^(10-r-4r)/2

= (-2)^r  10c_r x^(10-5r)/2

Let T_{r + 1} be the constant term 

(10 - 5r)/2  =  0 ⇒ r = 2

T_{r + 1} = T_{2 + 1}

= (-2)^2  10c₂ x^(10-5(2))/2

¹⁰C₂  =  (10⋅9)/(2⋅1)

= 4(45x⁰)

Hence the constant term is 180

Let us see the next example on "General and middle terms in binomial theorem".

Example 2 :

Find the constant term in the expansion (2x² + 1/x)¹²

Solution :

T_(r+1) =  ⁿc_r x^(n-r) a^r

Comparing the given expression with the form (x + a)ⁿ, we get x = 2x², a = 1/x and n = 12

T_(r+1) =  ¹²c_r (2x²)^(12-r) (1/x)^r

 =  ¹²c_r (2^12-r)(x²)^(12-r) (x^-r)

 =  2^{12-r [12}c_r x^(24-3r)]

Let T_{r + 1} be the constant term 

24 - 3r  =  0 ⇒ r = 8

T_{r + 1} = T_{8 + 1}

=  2^{12-8 [12}c₈ x^24-3(8)]

=  2⁴ (495) x⁰  ==> 7920

So, the constant term is 7920.

Example 3 :

Find the middle term in the expansion of (3x - 2x²/3)⁸

Solution :

Here n = 8, that is even

So, the middle term  = T_{(n/2) + 1}

  =  T _{(8/2) + 1}

  =  T _{(4 + 1)}  ==>  T ₅

General term : 

T_(r+1) =  ⁿc_r x^(n-r) a^r

x = 3x, a = 2x²/3,  r = 4 and n = 8

T _{(4 + 1)}  =  ⁸c₄ (3x)^(8-4) (2x²/3)⁴

  =  (8 ⋅ 7 ⋅ 6 ⋅ 5)/ (4 ⋅ 3 ⋅ 2 ⋅ 1)(3x)⁴ (2x²/3)⁴

  =  (8 ⋅ 7 ⋅ 6 ⋅ 5)/ (4 ⋅ 3 ⋅ 2 ⋅ 1)(3x)⁴ (2x²/3)⁴

  =  70(81x⁴)(16x⁸/81)

  =  70(16)x¹²

  =  1120x¹²

Example 4 :

Find the middle term in the expansion of (b/x  - x/b)¹⁶.

Solution :

Here n = 16, that is even

So, the middle term  = T_{(n/2) + 1}

  =  T _{(16/2) + 1}

  =  T _{(8 + 1)}  ==>  T ₉

General term : 

T_(r+1) =  ⁿc_r x^(n-r) a^r

x = b/x, a = x/b,  r = 8 and n = 16

T _{(8 + 1)}  =  ¹⁶c₈ (b/x)^(16-8) (x/b)⁸

  =  ¹⁶c₈ (b/x)⁸ (x/b)⁸

  = ¹⁶c₈

Example 5 :

Find the middle term in the expansion of (a/x  - √x)¹⁶

Solution :

Here n = 16, that is even

So, the middle term  = T_{(n/2) + 1}

  =  T _{(16/2) + 1}

  =  T _{(8 + 1)}  ==>  T ₉

General term : 

T_(r+1) =  ⁿc_r x^(n-r) a^r

x = a/x, a = - √x,  r = 8 and n = 16

T _{(8 + 1)}  =  ¹⁶c₈ (a/x)^(16-8) (- √x)⁸

  =  ¹⁶c₈ a⁸ x^-8 

  =  ¹⁶c₈ a⁸ x^-4

  =  ¹⁶c₈ a⁸/x⁴

Example 6 :

Find the middle term in the expansion of (x  - 2y)¹³

Solution :

Here n = 13, that is even

So, the middle term  =  T_{(n + 1)/2} and T_{(n + 3)/2}

T_{(n + 1)/2   =}   T _{(13+1)/2  ==>}  T ₇

General term : 

T_(r+1) =  ⁿc_r x^(n-r) a^r

x = x, a = -2y,  r = 6 and n = 13

T _{(6 + 1)}  =  ¹³c₆ (x)^(13-6) (-2y)⁶

  =  ¹³c₆ x⁷ (-2)⁶ y⁶

  =  ¹³c₆ x⁷ 2⁶ y⁶

T_{(n + 3)/2   =}   T _{(13+3)/2  ==>}  T ₈

x = x, a = -2y,  r = 7 and n = 13

T _{(7 + 1)}  =  ¹³c₆ (x)^(13-7) (-2y)⁷

  =  ¹³c₆ x⁶ (-2)⁷ y⁷

  = - ¹³c₆ x⁶ 2⁷ y⁷

Example 7 :

Find the middle term in the expansion of (x  + 2/x²)¹⁷

Solution :

Here n = 17, that is even

So, the middle term  =  T_{(n + 1)/2} and T_{(n + 3)/2}

T_{(n + 1)/2   =}   T _{(17+1)/2  ==>}  T ₉

General term : 

T_(r+1) =  ⁿc_r x^(n-r) a^r

x = x, a = 2/x²,  r = 8 and n = 17

T _{(8 + 1)}  =  ¹⁷c₈ (x)^(17-8) (2/x²)⁸

  =  ¹⁷c₈ x⁹ (2)⁸ x^-16

  =  ¹⁷c₈ x^9-16 2⁸

  =  ¹⁷c₈ x^-7 2⁸

  =  ¹⁷c₈ (2⁸/x⁷) 

T_{(n + 3)/2   =}   T _{(17+3)/2  ==>}  T ₁₀

x = x, a = 2/x²,  r = 9 and n = 17

T _{(9 + 1)}  =  ¹⁷c₉ (x)^(17-9) (2/x²)⁹

  =  ¹⁷c₉ (x)⁸ (2⁹/x¹⁸)  

=  ¹⁷c₉ (x)⁸ (2⁹x^-18)

=  ¹⁷c₉ (x)^8-18 2⁹

=  ¹⁷c₉ x^-10 2⁹

=  ¹⁷c₉ (2⁹/x¹⁰)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.