GEOMETRIC MEAN THEOREM LEG RULE

In every right triangle, a leg is the geometric mean between the hypotenuse and the projection of that leg on it .

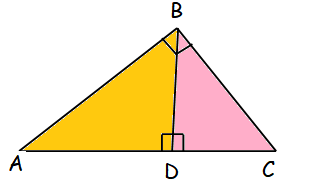
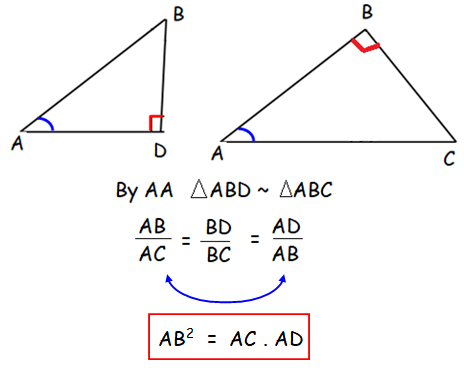
Result 1 :

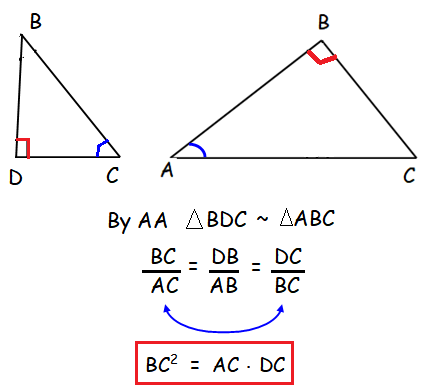
Result 2 :

Problems on Geometric Mean Theorem Leg Rule

Problem 1 :

Find x and y.

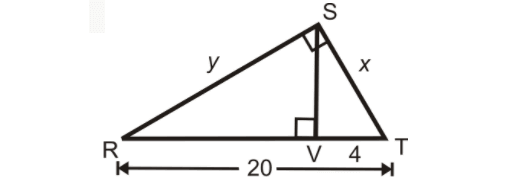
Solution :

From the results given above,

Problem 2 :

Find x and y.

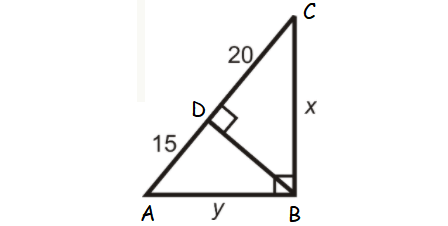
Solution :

AC  =  AD + DC

AC  =  15 + 20  ==>  35

x²  =  DC ⋅ AC

x²  =  20 ⋅ 35

x  =  √20 ⋅ 35

x  =  10√7

Problem 3 :

Find y.

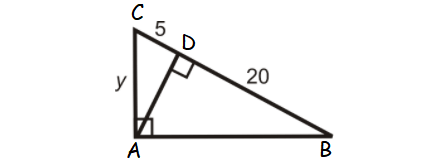
Solution :

BC  =  BD + DC

BC  =  20+5  ==>  25

AC²  =  CD ⋅ BC

AC  =  √(5 ⋅ 25)

AC  =  5√5

y  =  5√5

Problem 4 :

Find x.

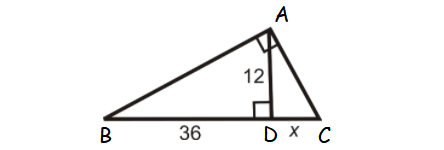
Solution :

AD²  =  BD ⋅ DC

12²  =  36 ⋅ x

144  =  36x

x  =  144/36

x  =  4

Problem 5 :

Find x, y and z.

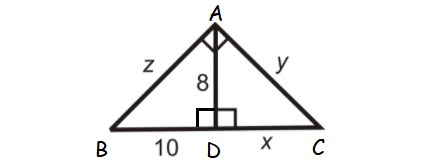
Solution :

In triangle ADB,

AB²  =  BD² + AD²

z²  =  10² + 8²

z²  =  164

z  =   √164

z  =  2 √41

AD²  =  BD ⋅ DC

8²  =  10 ⋅ x

x  =  64/10

x  =  6.4

AC²  =  AD² + DC²

y²  =  8² + (6.4)²

 y²  =  64 + 40.96

 y²  =  104.96

y  =  √104.96

y  =  10.24

Problem 6 :

Find x, y and z.

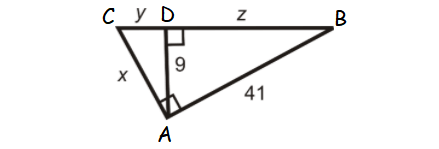
Solution :

In triangle ADB,

AB²  =  AD² + DB²

41²  =  9² + DB²

1681-81  =  DB²

DB  =  √1600

z  =  40

AD²  =  CD ⋅ DB

9²  =  y ⋅ z

81  =  40y

y  =  81/40

y  =  2.025

In triangle ADC,

AC²  =  CD²+DA²

AC²  =  y²+9²

AC²  =  (2.025)²+9²

AC²  =  4.1+81

AC²  =  85.1

AC  =  √85.1

AC  =  9.2

x  =  9.2

Problem 7 :

Exercises a–c, use the diagram at below

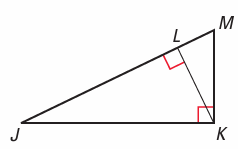
a) In the diagram, KL is the ? of ML and JL.

b) Complete the following statement:

ΔJKL~ Δ ? ~ Δ ?

c) Which segment’s length is the geometric mean of ML ?

Solution :

a) Here KL is the perpendicular for ML and JL.

b)  Considering triangles JKL and JMK,

∠LJK = ∠MJK (Shares common angle)

∠JLK = ∠JKM (90 degree)

Using AA, triangles JKL and JMK.

Considering triangles JKL and MLK

∠JMK = ∠LMK (Shares common angle)

∠JLK = ∠JKM (90 degree)

Using AA, triangles JKL and MLK.

From the above, we understand 

ΔJKL~ Δ JMK ~ Δ MLK

c) Triangles JKM and LJK are similar, then

MK/LK = JM/JK = JK/JL

JK² = JM ⋅ JL

JM and JL are geometric mean for JK.

Problem 7 :

You and a friend want to know how much rope you need to climb a large rock. To estimate the height of the rock,  As shown at the below, your friend uses a square to line up the top and the bottom of the rock. You measure the vertical distance from the ground to your friend’s eye and the distance from your friend to the rock. Estimate the height of the rock.

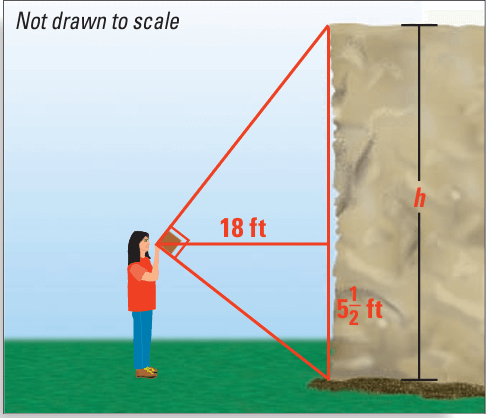
Solution :

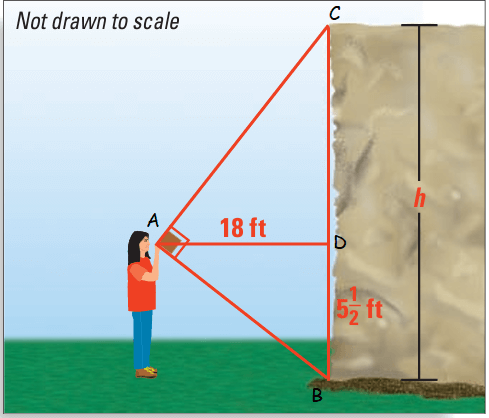
In triangles ACD, ADB

∠CAD = ∠DBA

∠BAD = ∠DCA

CD/AD = AD/DB

DB = 5  1/2 = 5.5

(h - 5.5)/18 = 18/5.5

(h - 5.5)5.5 = 18(18)

h - 5.5 = 324/5.5

h - 5.5 = 58.9

h = 58.9 + 5.5

h = 64.4

So, the value of h is 64 ft.

Problem 8 :

Zach wants to order a banner that will hang over a side of high school baseball stadium grandstand and reach the ground.

To find this height, he uses a cardboard square of line up to the top and bottom of the grandstand. He measures his distance from grandstand from the ground to his eye level. Find the height of the grandstand to the nearest foot.

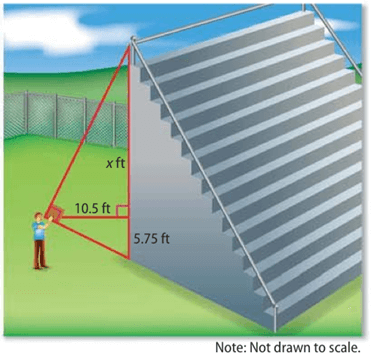
Solution :

x/10.5 = 10.5/5.75

x(5.75) = 10.5(10.5)

x(5.75) = 110.25

x = 110.25/5.75

x = 19.17

So, the required value of x is 19.17 feet.

The height of the grandstand is the total length of hypotenuse = 5.75 + 19.17

Then it is about 25 feet.

Problem 9 :

Corey is visiting the Jefferson memorial with his family. He wants to estimate the height of the statue of Thomas Jefferson. Corey stands so that his line of vision to the top and base of the statue from a right angle as shown in the diagram, about how tall is the statue ?

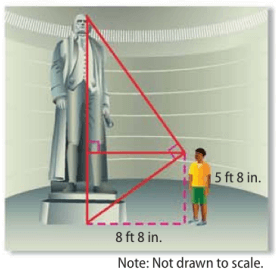
Solution :

Height of the boy = 5 ft 8 inches

1 ft = 12 inches

= 5(12) + 8

= 60 + 8

= 68 inches

horizontal distance between statue and boy :

= 8 ft 8 inches

= 8(12) + 8

= 96 + 8

= 104 inches

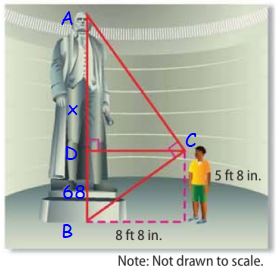
DC/AD = DB/DC

104/x = 68/104

(104)² = 68 x

x = (104)² / 68

x = 10816/68

x = 10816/68

x = 159

Total height of statue = 159 + 68

= 227 ft

= (216 + 11) ft

= 18 ft 11 inches

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.