GRADE 10 MATH PRACTICE QUESTIONS

Problem 1 :

AB and CD are two chords of a circle which intersect each other externally at P. If AB  =  4 cm, BP  =  5 cm, PD = 3 cm, then the length of CD is.

Solution :

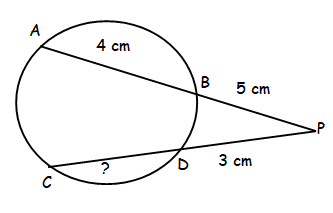
PA ⋅ PB  =  PC ⋅ PD

Let x be CD.

PA  =  9 cm, PB  =  5 cm, PC  =  3 + x and PD  =  3 cm

9 ⋅ 5  =  (3 + x) ⋅ 3

15  =  3 + x

x  =  15 - 3

x  =  12

So, CD is 12 cm.

Problem 2 :

Find a if the slope of the line joining (-6, 13) and (3, a) is -1/3

Solution :

Slope of the line  =  (y₂ - y₁)/(x₂ - x₁)

(a - 13) / (3 + 6)  =  -1/3

(a - 13) / 9  =  -1/3

a - 13  =  -3

a  =  -3 + 13

a  =  10

So, the value of a is 10.

Problem 3 :

Two dice are thrown together. What is the probability of getting a total 8 or a product 12.

Solution :

Sample space  = 

{(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) 6 (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) }

n(s)  =  36

Let A and B are the events of the sum 8 or the product is 12.

A  =  {(2, 6) (3, 5) (4, 4) (5, 3) (6, 2)} 

n(A)  =  5

p(A)  =  n(A)/n(S)

p(A)  =  5/36

B  =  { (2, 6) (3, 4) (4, 3)(6, 2) }

n(B)  =  4

p(B)  =  4/36

A n B  =   {(2, 6) (6, 2)}

n(A n B)  =  2

p(A n B)  =  n(A n B) / n(S)

p(A n B0  =  2/36

P(A u B)  =  p(A) + p(B) - p(A n B)

   =  5/36 + 4/36 - 2/36

  =  (9 - 2)/36

  =  7/36

So, the probability of getting the sum 8 or the product as 12 is 7/36.

Problem 4 :

The line joining the points (-2, 7) and (3, 6) is parallel to the line joining (4, a) and (9, 1), find a.

Solution :

If two lines are parallel, they will have equal slopes.

Let the given points as A(-2, 7), B(3, 6), C(4, a) and D(9, 1)

Slope of line AB  =  Slope of line CD

 Slope of the line joining two points  =  (y₂ - y₁)/(x₂ - x₁)

(6 - 7) / (3 + 2)  =  (1 - a)/(9 - 4)

-1/5  =  (1 - a)/5

-1  =  1 - a

a  =  1 + 1

a  =  2

So, value of a is 2.

Problem 5 :

Find the range of the heights of 12 girls in the class given in cm 

120, 110, 150, 100, 130, 145, 150, 100, 140, 150, 135, 125

Solution : 

Range  =  Large value - Small value

L  =  150 and S  =  100

Range  =  150 - 100

Range  =  50

Problem 6 :

The volume of a cylinder is 448π cm and its height is 7 cm.Find the radius of the cylinder.

Solution :

Volume of cylinder  = πr² h

πr² h  =  448 π

Height of the cylinder(h)  =  7 cm

  r² (7)  =  448 

  r²  =  64

  r  =   8

So, the radius of the cylinder is 8 cm.

Problem 7 :

How many terms of a series

1 + 6 + 11 + ............ 

must be taken so that their sum is 970?

Solution :

Sn  =  970

(n/2) [2a + (n -1) d]  =  970

a  =  1, d  =  6 - 1  ==>  5

(n/2) [2(1) + (n -1) 5]  =  970

(n/2) [2+5n-5]  =  970

(n/2) (-3 + 5n)  =  970

-3n + 5n²  =  970(2)

 5n² - 3n  - 1940   =  0 

((n - 20) (5n + 97)  =  0

n  =  20 and n  =  -97/5

So, 20 terms must be taken to have the sum 970.

Problem 8 :

Find the values of k for which the equation

12x²+4kx+3  =  0

has real and equal roots.

Solution :

Since the quadratic equation has real and equal roots

Discriminant  =  0

b² - 4ac  =  0

a  =  12, b  =  4k and c  =  3

(4k)² - 4(12)(3)  =  0

16k² - 144  =  0

k² - 9  =  0

k² - 3²  =  0

(k + 3) (k - 3)  =  0

k  =  -3 and k  =  3

So, the value of k is -3 or 3.

Problem 9 :

The sum of three numbers is 24.Among them one number is equal to half of the sum of the other two numbers but four times the difference of them. Find the numbers.

Solution :

Let x, y and z be the three numbers.

x+y+z  =  24  ---(1)

x  =  (y+z) / 2

2x-y-z  =  0 -----(2)

x  =  4(y-z)

x  =  4y-4z

x-4y+4z  =  0-----(3)

(1) + (2)

3x  =  24

x  =  8

By applying the value of x in (2), we get

16-y-z  =  0

y+z  =  16  ----(4)

By applying the value of x in (3), we get

8-4y+4z  =  0

y-z  =  2 ----(5)

(4) + (5)

2y  =  18

y  =  9

By applying the value of y in (5), we get

9-z  =  2

z  =  7

So, the required numbers are 8, 9 and 7.

Problem 10 :

A ladder 17 m long touches a window of a house 15 m above the ground. Determine the distance of the floor of the ladder from the house.

Solution :

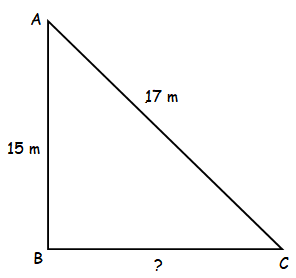
AC²  =  AB² + BC²

17²  =  15² + BC²

289 - 225  =  AC²  

 AC  =  8

So, the ladder is at the distance of 8 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.