GRADE  10 MATH QUESTIONS AND SOLUTIONS

Problem 1 :

Find greatest common factor of the following terms 

20x³, 36x⁶

Solution :

20  =  2² ⋅ 5

36  =  2² ⋅ 3²

Greatest common factor  =  2² ⋅ 3² ⋅ 5

  =  180

So, the greatest common factor is 180x⁶.

Problem 2 :

Simplify the following

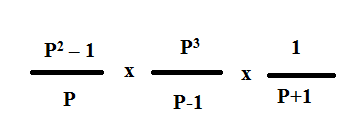
Solution :

p² - 1  =  (p+1) (p-1)

  =  [(p+1) (p-1)/p]⋅ [p³/(p-1)] ⋅ [1/(p+1)]

  =  p²

Problem 3 :

Find the square root of 9801 by factor method.

Solution :

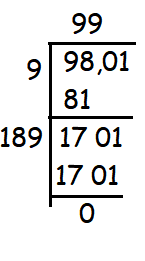
So, the square root of 9801 is 99.

Problem 4 :

Solve 6x² + x - 1  =  0

Solution :

6x² + x - 1  =  0

(3x - 1) (2x + 1)  =  0

So the solution is {-1/2, 1/3}.

Problem 5 :

The product of two consecutive odd number is 323. Find them.

Solution :

Let x and x + 2 are two consecutive odd numbers. 

Product of two consecutive odd numbers =  323

x (x + 2)  =  323

x² + 2x  =  323

x² + 2x - 323  =  0

(x - 17)(x + 19)

x  =  17 and x  =  -19

So, the two odd numbers are 17 and 19.

Problem 6 :

Find two consecutive even integers whose product is 224.

Solution :

Let x and x + 2 are two consecutive even integers.

Product of even integers  =  224

x(x + 2)  =  224

x² + 2x  =  224

x² + 2x - 224  =  0

(x + 16) (x - 14)  =  0

x  =  -16 and x  =  14

So, two consecutive even numbers are 14 and 16.

Problem 7 :

The length of the hall is 3 m more than its width. The numerical value of its area is equal to the numerical value of its perimeter. Find the length and width of the hall.

Solution :

Let x be the width of the hall

length  =  x + 3

Area of the hall  =  Perimeter of the hall

x(x+3)  =  2(x+x+3)

x² + 3x  =  2(2x+3)

x² + 3x - 4x - 6  =  0

x² - 1x - 6  =  0

(x - 3)(x + 2)  =  0

x  =  3 and x  =  -2

x + 3  =  6

So, the width and length of the rectangle are 3 and 6 m. 

Problem 8 :

Find the area of the sector of a circle with radius 4 cm and of angle 30°. Also, find the area of the corresponding major sector approximately (use π = 3.14).

Solution :

Area of major sector  =  πr² - (θ/360)πr²

  =  π4² - (30/360)π4²

  =  π4²(1 - 1/12)

  =  π4²(11/12)

  =  (176/12)(3.14)

  =  46.05 cm²

Problem 9 :

OACB is a quadrant of a circle with center O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region. 

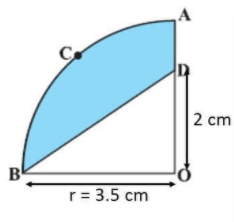
Solution :

Area of shaded region   =  Area of quadrant - Area of triangle ODB

  =  πr² - (1/2) ⋅ base ⋅ height

  =  (22/7)(3.5)² - (1/2) ⋅ 3.5 ⋅ 2

  =  38.5 - 3.5

  =  35 cm²

Problem 10 :

The wheels of a car are of diameter 80 cm each. Find how many complete revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour.

Solution :

Speed of the car  =  66 km/hr

 1000 m  =  1 km

  100 cm  =  1 m

66 km  =  6600000 cm

66 km/hr  =  6600000/60

  =  110000 cm/min

Distance covered  =  Time (Speed)

  =  10(110000)

  =  1100000 

Radius of the wheel  =  40 cm

Number of revolutions

  =  Distance covered / Distance covered by 4 wheels

Distance covered by 4 wheels  =  2πr

  =  1100000 / [2 (3.14) ⋅ 40]

=  1100000/251.2

  =  4379

So, each wheel has to revolve 4379 times.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.