GRADE 10 MATH WORKSHEET WITH ANSWER

Problem 1 :

The sides of the triangle are (x-1), x and (x+1). Find the sides of the triangle.

Solution :

Since the given are sides of the right triangle, the longest side is the hypotenuse.

(x+1)²  =  (x-1)² + x²

x²+2x+1  =  x²-2x+1+x²

x²-4x  =  0

x(x-4)  =  0

x  =  0 and x  =  4

So, the sides of the triangle are 3, 4 and 5.

Problem 2 :

If A  =  {a, b, c, d, e, f, g, h} ,B  =  {a, b, e, f} and C  =  {a, c, e, g, h, k} find A - (B∪C).

Solution :

B∪C  =  {a, b, c, e, f, g, h, k}

A - (B∪C)  =  {a, b, c, d, e, f, g, h} - {a, b, c, e, f, g, h, k}

A - (B∪C)  =  {d}

Problem 3 :

What month is 19 months after July ?

Solution :

July corresponds to 7 in month arithmetic. 

We want to know the day which is  19 months after July. 

7 + 19  =  26

By dividing 26 by 12, we get 2 as remainder.

2 corresponds to February

So, the month which is after 19 months will be February.

Problem 4 :

A G.P consists of even number of terms. If sum of all the terms is three times of the odd number. Find the common ratio.

Solution :

Let the required geometric progression is having 4 terms.

a, ar, ar², ar³

s_n  =  a(1-rⁿ)/(1-r)

Sum of above four terms :

s₄  =  a(1-r⁴)/(1-r)

Sum of odd terms :

a + ar²

=  a(1+r²)

Sum of all terms  =  3(sum of odd terms)

a(1-r⁴)/(1-r)  =  3a(1+r²)

(1+r²)(1-r²)/(1-r)  =  3(1+r²)

(1+r)(1-r)/(1-r)  =  3

1+r  =  3

r  =  2

So, the common ratio is 2.

Problem 5 :

A rocket is in the form of a cylinder surmounted by a cone.The cylinder is of radius 2.5 m and the height 21 m and the cone has the slant height 6.5 m. Calculate the surface area of the rocket.

Solution :

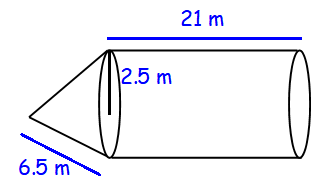
Surface area of rocket  =  Curved surface area of cone + curved surface area of cylinder

  =  πrl + 2πrh

  = πr(l+2h)

  = (22/7) 2.5 (6.5+24)

  = (22/7) 2.5 (30.5)

  =  239.64

Problem 6 :

Find the value of a and b if ax³+bx²+7x+9 and x³+ax²-2x+b-4 when divided by x + 2 leave the remainders -13 and -16 respectively.

Solution :

Let p(x)  =  ax³+bx²+7x+9 and q(x)  =  x³+ax²-2x+b-4

x+2  =  0

x  =  -2

p(-2)  =  a(-2)³+b(-2)²+7(-2)+9

-13  =  -8a+4b-14+9

-8a+4b  =  -13 + 5

-8a+4b  =  -8

Dividing by -4, we get

2a - b  =  2 -----(1)

q(x)  =  x³+ax²-2x+b-4

q(-2)  =  (-2)³+a(-2)²-2(-2)+b-4

-16  =  -8+4a+4+b-4

4a + b  =  -16+8

4a + b  =  -8 -----(2)

(1) + (2)

6a  =  -6

a  =  -1

By applying the value of a in (1), we get

-2-b  =  2

-b  =  4

b  = -4

So, the values of a and b are -1 and -4.

Problem 7 :

Find the square root of 15625

Solution :

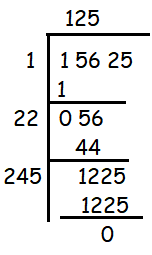
So, square root of 15625 is 125.

Problem 8 :

Determine the nature of the roots of the equation

x²-2x+5   =  0

Solution :

Nature of roots  =  b² - 4ac

a  =  1, b  =  -2 and c  =  5

  =  (-2)² - 4(1)(5)

  =  4 - 20

  =  -16 < 0

It has no real roots. 

Problem 9 :

Two poles of heights 6 m and 11 m stand on a plane ground. The distance between their feet is 12 m, find the distance  between the tops.

Solution :

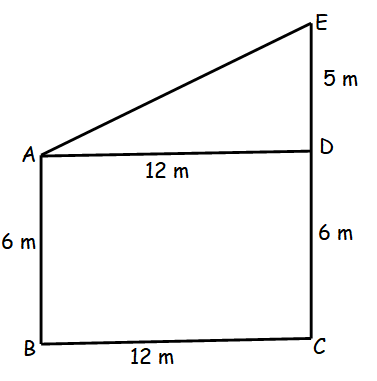
Distance between two poles  =  AE

In triangle ADE, 

AE²  =  AD² + DE² 

AE²  =  12² + 5² 

AE²  =  144+25

AE²  =  169

AE  =  13

So, the distance between two poles.

Problem 10 :

Find the point which divides the line segment joining the points (2, 1) and (3, 5) externally in the ratio 2:3

Solution :

Required point  =  (lx_2-mx₁)/(l-m), (ly_2-my₁)/(l-m)

  =  [2(3)-3(2)]/(2-3), [2(5)-3(1)]/(2-3)

  =  (6-6)/5, (10-3)/(-1)

  =  (0, -7)

So the required point is (0, -7).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.