GRADE 8 MATH PRACTICE QUESTIONS

Question 1 :

Find the smallest number by which 3087 should be multiplied to obtain a perfect cube. 

(A)  4              (B)  3               (C)  5 

Solution :

By finding the prime factors of 3087, we know that

=  ∛(3 ⋅ 3 ⋅ 7 ⋅ 7 ⋅ 7) So, 3 is the smallest number to be multiplied to obtain a perfect cube.

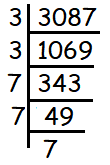Question 2 :

11025 students are sitting in a lawn in such a way that there are many students in a row as there are rows in lawn. Find the number of rows in the lawn.

(A)   205              (B)   105           (C)   115

Solution :

From the given information, we come to know that the number of rows in the lawn is equal to the number of students in a row.

Then we should find the square root of 11025.

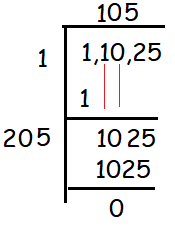
So, the number of rows in the lawn is 105.

Question 3 :

Evaluate (243) ^-2/5 

(A)   1/5             (B)   1/7           (C)   1/9

Solution :

(243) ^-2/5   

243  =  3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3  =  3⁵

(243) ^-2/5    =  (3⁵)^-2/5

  =  3^-2

  =  1/3²  =  1/9

Question 4 :

Evaluate (5² + 12²)^1/2

(A)  17          (B)   15         (C) 13

Solution :

(5² + 12²)^1/2 =  (5² + 12²)^1/2

  =  (25 + 144)^1/2

  =  √169

  =  √(13 ⋅ 13)

  =  13

Question 5 :

If a + b + c  =  9 and ab + bc + ca  =  23, find the value of a² + b² + c²

(A)  35        (B)  45         (C)  55

Solution :

 (a + b + c)²  =  a² + b² + b² + 2ab + 2bc + 2ca

 (a + b + c)²  =  a² + b² + b² + 2(ab + bc + ca)

 9²  =  a² + b² + b² + 2(23)

81  =  a² + b² + b² + 46

  81 - 46  =  a² + b² + b²

a² + b² + b²  =  35

Question 6 :

What is the degree of the polynomial 4 + 3x - 7x³ + 5x⁴

(A)  4         (B)  3        (C)  1

Solution :

The highest power of the polynomial is know as degree.

So, the degree of the polynomial is 4.

Question 7 :

Solve the following 3x / (2x - 5) = 12/5

(A)  20/3    (B)  10/7     (C)  15/8

Solution :

3x / (2x - 5)  =  12/5

5(3x)  =  12 (2x - 5)

15x  =  24 x - 60

15x - 24x  =  -60

-9x  =  -60

x  =  60/9

x  =  20/3

So, the required fraction is 20/3.

Question 8 :

The numerator of a rational number is less than its denominator by the number 3. If the numerator becomes three times and the denominator is increased by 20, the new fraction became 1/8. Find the required fraction. 

(A)  1/3                (B)   1/2              (C)   1/4

Solution :

Let x  =  denominator

x-3  =  numerator

3 (x-3) / (x+20) = 1/8

(3x-9) / (x+20) = 1/8

8(3x-9) = (x+20)

24x - 72  =  x + 20

Subtract both sides by x 

24x - x  - 72  =  20

Add both sides by 72 

23x  =  20 + 72

x  =  92/23  =  4 (denominator)

Numerator  =  4 - 3  =  1

Hence the required fraction is 1/4.

Question 9 :

In a circle with center O and the radius 13 cm, AB is a chord of length 24 cm. Find the distance between the chord and the center.  

(A)  6 cm               (B)   8 cm              (C)   5 cm

Solution :

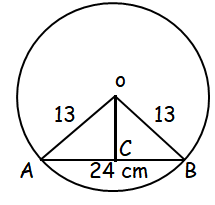
In triangle OCB,

OB²  =  OC² + CB²

OC bisects the chord.

13²  =  OC² + 12²

OC²  =  169 - 144

OC²  =  25

OC  =  5 cm

So, the distance between center and the chord is 5 cm.

Question 10 :

Find the value of x° if the lines AB and CD are parallel to each other

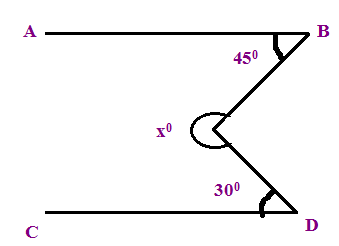
(A)   0°               (B)   180°            (C)   225°

Solution :

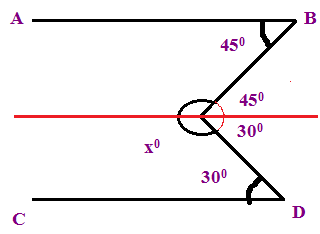
x  =  360 - (45 + 30)

x  =  360 - 75

x  =  285

So, the required angle is 285.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.