GRADE 9 MATH PRACTICE QUESTIONS

Problem 1 :

Find the area of the shaded region.

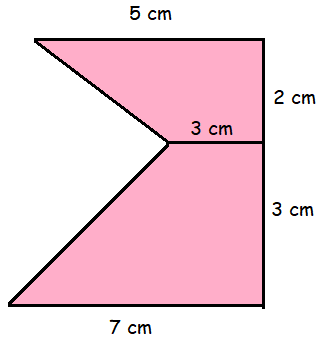
Solution :

Area of trapezoid  =  (1/2) h(a+b)

h - height, a and b are parallel sides.

Area of large trapezoid  =  (1/2) 3(7+3)

  =  (1/2) 3(10)

  =  15

Area of small trapezoid  =  (1/2) 2(5+3)

  =  8

Problem 2 :

Solve log₆ 2x - log₆ (x + 1)  =  0

Solution :

 log₆ [2x/(x-1)]  =  0

2x/(x-1)  =  6⁰

2x/(x-1)  =  1

2x  =  x-1

2x-x  =  -1

x  =  -1

So, the value of x is -1.

Problem 3 :

The number of girls in a village who attended tailoring classes was 45, he number of girls who attended classes on gardening was 70. If 30 of these attended both the classes find how many totally attended either of these classes.

Solution :

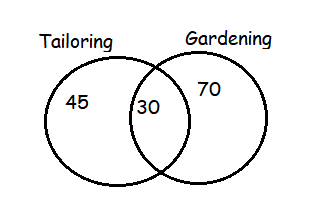
Number of girls who attened only tailoring  =  45 - 30

  =  15

Number of girls who attened only tailoring  =  70 - 30

  =  40

The number of students totally attended either of these classes

  =  15 + 40 + 30

=  85

Problem 4 :

If the values of a-b and ab are 6 and 40 respectively, find the values of a² + b²

Solution :

a-b  =  6 and ab  =  40

(a-b)²  =  a²-2ab+b²

a²+b²  =  (a-b)² + 2ab

a² + b²  =  (6)² + 2(40)

  =  36 + 80

a² + b²  =  116

Problem 5 :

Two non intersecting lines are called _____________

Solution :

Two non intersecting lines are called as parallel lines.

Problem 6 :

Find the value of x and y in the below picture.

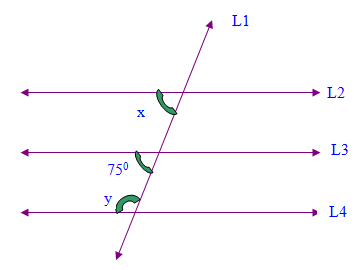
Solution :

x  =  75

y + 75  =  180

y  =  180 - 75

y  =  105

Problem 7 :

If n(A)  =  5, find n[p(A)] 

Solution :

n(p(A))  =  2 ^n(A)

n(p(A))  =  2⁵

n(p(A))  =  32

Problem 8 :

If no sides of a triangle are of equal length, then the triangle is called ____________ triangle.

Solution :

In scalene triangle all three sides will have different length.

Problem 9 :

If 2 sin(A+B)  =  √3 and √2cosB  =  1, find A and B.

Solution :

2 sin(A+B) = √3 --------(1)

 √2cosB = 1 ------(2)

From (1),

sin(A+B) = √3/2

A+B  =  60  ---(3)

From (2)

 √2cosB = 1 

cosB  =  1/√2

B  =  45

By applying the value of B in (3), we get

A + 45  =  60

A  =  60 - 45

A  =  15

Problem 10 :

Two adjacent angles are said to be complementary angles if the sum of their measures is ______

Solution :

If the sum of two angles is 90 degree, then they are known as complementary angle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.