GRADE 9 MATH TEST WITH ANSWERS

Problem 1 :

Which is bigger ³√3 or ⁵√4

Solution :

To compare the above radical terms having different index, we should change them having the same index.

Least common multiple (3 and 5) is 15.

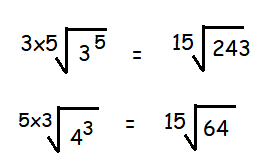
Now we can compare the values inside the radical sign and decide which is greater and which is smaller.

³√3 > ⁵√4

Problem 2 :

Simplify √64 + √2500

Solution :

√64  = √(2⋅2⋅2⋅2⋅2⋅2)  =  8

√2500  = √(5⋅5⋅5⋅5⋅2⋅2)  =  50

  =  8 + 50

  =  58

√64 + √2500  =  58

Problem 3 :

√3 + √2 and √3 - √2 are called ____________ surds.

Solution :

√3 + √2 and √3 - √2 are called conjugate surds.

Problem 4 :

Two sets are called __________________ sets if they have the same number of elements. 

Solution :

If two sets are having same number of elements, they will be known as equal sets.

Problem 5 :

Find the angle of a sector whose radius is 21 cm and length of the arc is 66 cm.

Solution :

Radius  =  21 cm, arc length  =  66 cm

(θ/360)2πr  =  66

(θ/360)2⋅(22/7) ⋅21  =  66

θ  =  180

So, the required angle is 180.

Problem 6 :

The ratio of area of quadrant of the circle to the area of the semi circle is.

Solution :

In a semi circle, there must be two equal parts and quadrant is one fourth of the circle. But in semi circle it is half of the circle.

So, the required ratio is 1 : 2.

Problem 7 :

Find the area of the shaded portion if radius of the circle OA measures 7 cm and AB = DC = 7 cm.

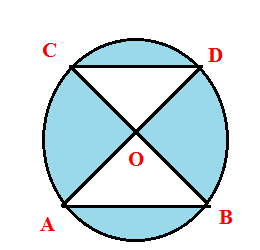
Solution :

OA  =  OB  =  OC  =  OD  =  7 cm (radii)

AB  =  CD  =  7 cm

OAB is a equilateral triangle.

Area of equilateral triangle  =  (√3/4)⋅a² 

 =  (√3/4)⋅7² 

Area of circle  =  πr²

=  (22/7)⋅7² 

Area of shaded region  =  (22/7)⋅7²   -  (√3/4)⋅7² 

  =  7² [(22/7) - (√3/4)]

  =  49(3.14 - 0.433)

  =  49(2.707)

  =  132.64 cm²

Problem 8 :

The equations 

3x-4y  =  6, -6x+8y  =  -12

has ______________ no of solution.

Solution :

a₁  =  3, a₂  =  -6

b₁  =  -4, a₂  =  8

c₁  =  -6, c₂  =  12

a₁/a₂  =  b₁/b₂  =  c₁/c₂

-3/6  =  -4/8  =  -6/12 ==>  -1/2

So, the linear equations are coincident and it will have infinitely many solution.

Problem 9 :

The point of concurrency of the altitudes of a triangle is called  ___________.

Solution :

The point of concurrency of the altitudes of a triangle is called orthocenter.

Problem 10 :

The sum of any adjacent angles of a parallelogram is equal to ________  

Solution :

The sum of any adjacent angles of a parallelogram is equal to 180 degree.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.