GRADE 9 MATH WORKSHEET

Problem 1 :

Find the value of a² if the value of a is

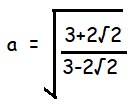
Solution :

a²  =  (3 + 2√2)/(3 - 2√2)

Multiplying by the conjugate of the denominator, we get

a²  =  [(3 + 2√2)/(3 - 2√2)] ⋅ [(3 + 2√2)/(3 + 2√2)]

a²  =  [(3 + 2√2)²/(3² - 2²√2²)]

a²  =  [(9 + 8 + 12√2)/(9 - 8)]

a²  = 17 + 12√2

Problem 2 :

If the length of the sides of a triangle are 11 cm, 60 cm and 61 cm, find the area of the triangle

Solution :

Side lengths of triangle :

a = 11 cm, b = 60 cm and c = 61 cm

Area of triangle = √s(s - a)(s - b)(s - c)

s = (a + b + c)/2

s = (11 + 60 + 61)/2

s = 66

s-a  =  66-11  ==>  55

s-b  =  66-60  ==>  6

s-c  =  66-61  ==>  5

Area of triangle  =  √s(s - a)(s - b)(s - c)

=  √(66⋅55⋅6⋅5)

=  11⋅6⋅5

Area of triangle  =  330 cm²

Problem 3 :

At a gathering of  30 people, there are 20 people who all know each other and 10  people who know no one. People who know each other hug, and people who do not know each other shake hands. How many handshakes occur within the group ?

Solution :

Number of people who do hand shakes  =  10

At a time two persons do handshake

10C₂ =  10!/(10-2)!2!

  =  10!/8!2!

  =  10⋅9⋅8!/8! 2⋅1

Total number of handshakes  =  45

Problem 4 :

Simplify log₃27 + log₃729 

Solution :

log₃27 + log₃729  =  log₃(27 ⋅ 729)

=  log₃(3⁴ ⋅ 3⁵)

=  log₃(3⁴⁺⁵)

=  log₃3⁹

 =  9(1)

 log₃27 + log₃729 = 9

Problem 5 :

If A and B be two sets. If every elements of A is also an element of B, then A is called a ____________ of B.

Solution :

Answer is subset.

Problem 6 :

If A = { 1, 2, 3, 4, 5, 6 } and B = { 1, 3, 7 } then the value of A-B ?

Solution :

To find A-B, we should ignore the common elements of A and B and list out the remaining elements of A.

A - B  =  {2, 4, 5, 6}

Problem 7 :

Find the product of (x + 3) (x + 5)

Solution :

(x + 3) (x + 5) = x² + 3x + 5x + 15

  = x² + 8 x + 15

Problem 8 :

If 2a - 3b = 2 and ab = 6 then 8a³ - 27b³

Solution :

8a³ - 27b³  =  (2a)³ - (3b)³

a³ - b³  =  (a-b)³+3ab(a-b)

  =  (2a-3b)³ + 3(2a)(3b)(2a-3b)

=  2³ + 18ab(2)

=  8 + 36(6)

  =  8 + 216

=  224

Problem 9 :

A pair of angles with a common vertex and common arm are called _________.

Solution :

A pair of angles with a common vertex and common arm are called adjacent angles.

Problem 10 :

Find in which quadrant does the point (-2,-3) lie?

Solution :

The given point is in the form (-x, -y), it lies in the third quadrant.

Problem 11 :

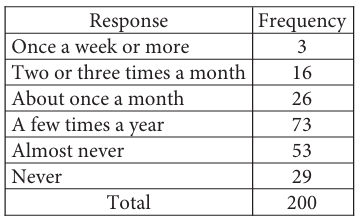
The table gives the results of a survey of 200 people who were asked how often they see a movie in a theater. How many people responded either “never” or “almost never”?

A) 24     B) 53     C) 82     D) 118

Solution :

Number of people responded either = 29

Number of people responded almost never = 53

Total number of people responded never or almost never

= 29 + 53

= 82

Problem 12 :

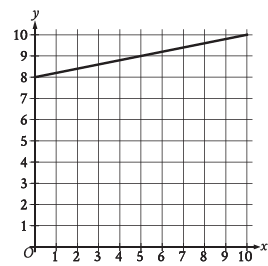
What is the y-intercept of the line graphed?

A) (0, −8)    B) (0, -1/8)    C) (0, 0)    D) (0, 8)

Solution :

y-intercept = 8

So, option D (0, 8) is correct.

Problem 13 :

Connor has c dollars and Maria has m dollars. Connor has 4 times as many dollars as Maria, and together they have a total of $25.00. Which system of equations represents this situation?

a) c = 4m, c + m = 25        b) m = 4c,  c + m = 25 

c) c = 25m, c + m = 4         d) m = 25c, c + m = 4

Solution :

Amount Connor has = c

Amount Maria has = m

c = 4m

Amount they have together = 25

m + c = 25

So, option a is correct.

Problem 14 :

Line k is defined by y = 3x + 15. Line j is perpendicular to line k in the xy-plane. What is the slope of line j ?

a) − 1/3     b) − 1/12   c) − 1/18    d) − 1/45

Solution :

Equation of line k :

y = 3x + 15

Line j is perpendicular to line k. 

Comparing with y = mx + b, we get m = 3. When two lines are perpendicular, the product of the slope of the line and slope of perpendicular line = -1

3 x slope of perpendicular line = -1

Slope of perpendicular line = -1/3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.