GRADIENT OF A STRAIGHT LINE

It is the change in y for a unit change in x along the line and usually denoted by the letter "m"

Gradient is also known as slope and it is sometimes referred to as "rise over run"

Because the fraction consists of the "rise" (the change in y, going up or down) divided by the "run" (the change in x, going from left to the right).

The figure given below illustrates this. 

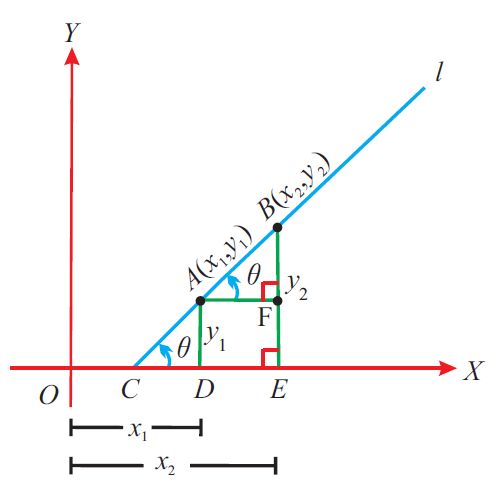
From the above figure, the gradient of the straight line joining the points A (x₁, y₁) and B (x₂, y₂) is   

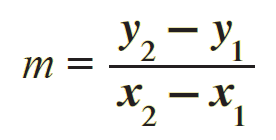
That is, 

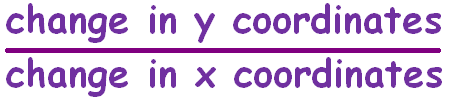
If the equation of a straight line given in general form

ax + by + c  =  0,   

then, the formula to find gradient of the line is 

Let θ be the angle between the straight line "l" and the positive side of x - axis.

The figure given below illustrates this. 

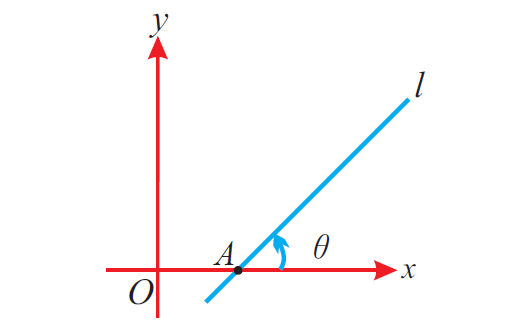
Then, the formula to find gradient of the line is

m  =  tan θ

In the general form of equation of a straight line

ax + by + c  =  0,

(i)  if "x" term is missing, then the line will be parallel to x - axis and its gradient will be zero.

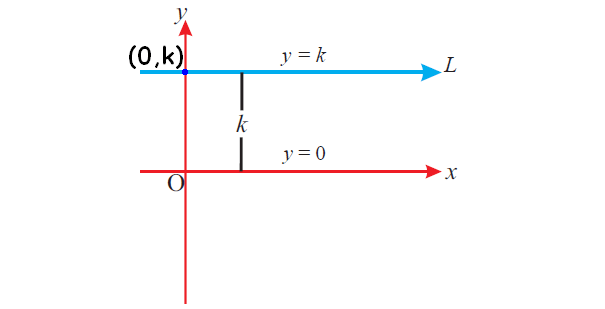
We know that gradient  =  change in y / change in x 

In the above figure, the value of "y" is fixed and that is "k"

So, there is no change in "y" and change in y = 0 

Gradient  =  0 / change in x  

Gradient  =  0 

(ii)  if "y" term is missing, then the line will be parallel to y - axis and its gradient will be undefined. 

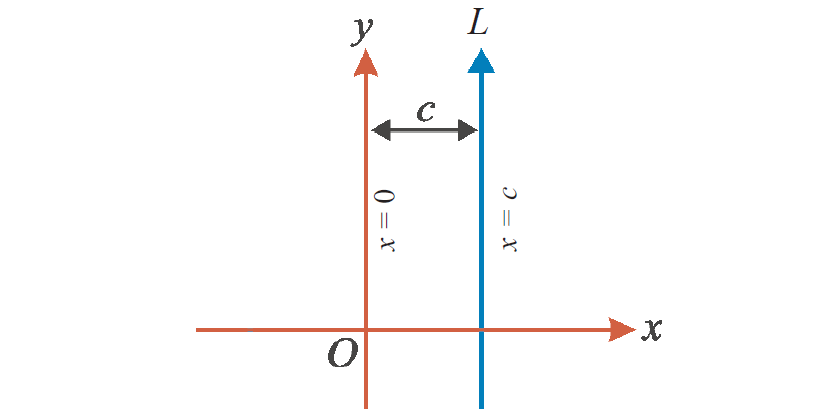
We know that gradient  =  change in y / change in x 

In the above figure, the value of "x" is fixed and that is "c"

So, there is no change in "x" and change in x = 0 

Gradient  =  change in y / 0   

Gradient  =  Undefined 

Gradient of the coordinate axes "x" and "y". 

(i)  Gradient of "x" axis zero.

(ii)  Gradient of "y" axis undefined. 

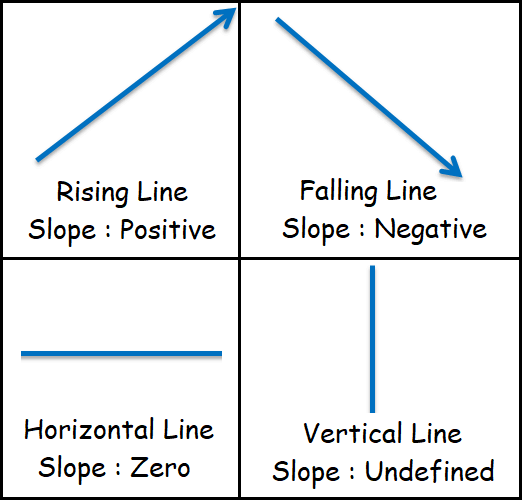
Gradient of a straight line - Positive or Negative or Zero or Undefined

To know the sign of the gradient of a straight line, always we have to look at the straight line from left to right. 

(i) If the line is going (from left to right) towards up, then the line is called rising line and its gradient or slope will be a positive value.

(ii) If the line is going (from left to right) towards down, then the line is called falling line and its gradient or slope will be a negative value.

(iii) If the line is horizontal, the gradient or slope will be zero. 

(iv) If the line is vertical, the gradient or slope will be undefined. 

Gradient of a Straight Line - Examples

Problem 1 :

Find the angle of inclination of the straight line whose gradient is 1/√3.

Solution :

Let θ be the angle of inclination of the line. 

Then, gradient of the line,  m  = tan θ.

Given : Gradient  =  1/√3.

So, we have 

tan θ  =  1/√3

θ  =  30°

So, the angle of inclination is 30°.

Problem 2 :

Find the gradient of the straight line passing through the points (3, -2) and (-1, 4). 

Solution :

Let (x₁, y₁)  =  (3, -2) and (x₂, y₂)   =  (-1, 4)

Then, the formula to find the gradient, 

m  =  (y₂ - y₁) / (x₂ - x₁)

Plug (x₁, y₁)  =  (3, -2) and (x₂, y₂)   =  (-1, 4)

m  =  (4 + 2) / (-1 - 3)

m  =  - 6 / 4

m  =  - 3 / 2

So, the gradient is -3/2.

Problem 3 :

Using the concept of gradient, show that the points A(5, -2), B(4, -1) and C(1, 2) are collinear.

Solution :

Slope of the line joining (x₁, y₁) and (x₂, y₂) is, 

m  =  (y₂ - y₁) / (x₂ - x₁)

Using the above formula,

Gradient of the line AB joining the points A (5, - 2) and B (4- 1) is 

 =  (-1 + 2) / (4 - 5)

=  - 1

Gradient of the line BC joining the points B (4- 1) and C (1, 2) is 

 =  (2 + 1) / (1 - 4)

=  - 1

Thus,

gradient of AB  =  gradient of BC

Also, B is the common point.

So, the points A , B and C are collinear.

Problem 4 :

Find the gradient of the line 3x - 2y + 7 = 0. 

Solution :

When the general form of equation of a straight line is given, the formula to find gradient is

m  =  -  coefficient of x / coefficient of y 

In the given line 3x - 2y + 7 = 0,

coefficient of x  = 3 and coefficient of y  =  - 2

Gradient,  m  =  (-3) / (-2)  =  3/2 

So, the gradient of the given line is 3/2. 

Problem 5 :

If the straight line 5x + ky - 1 = 0 has the gradient 5, find the value of 'k'.  

Solution :

When the general form of equation of a straight line is given, the formula to find gradient is

m  =  -  coefficient of x / coefficient of y 

In the given line 3x - 2y + 7 = 0,

coefficient of x  = 3 and coefficient of y  =  k

Slope,  m  =  -5 / k

Given : Gradient  =  5

So, we have  5  =  -5/k

5k  =  -5

k  =  -1

So, the value of 'k' is  -1. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.