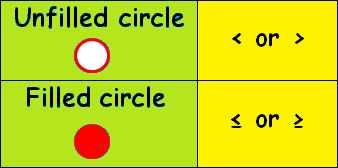
GRAPH INEQUALITIES ON A NUMBER LINE

1. If we have the inequality

< (less than) or > (greater than),

we have to use the empty / unfilled circle.

2. If we have the inequality sign 

≤ (less than or equal to) or ≥ (greater than or equal to),

we have to use the filled circle.

Example 1 :

Solve the following linear inequality and graph.

2x - 4 ≤ 0

Solution :

2x - 4 ≤ 0

Add 4 on both sides

2x - 4 + 4 ≤ 0 + 4

2x ≤ 4

Divide by 2 on both sides

2x/2 ≤ 4/2

x ≤ 2

So, any real number less than or equal to 2 is a solution of the given equation.

The solution set of the given inequality is (-∞, 2].

Example 2 :

Solve the following linear inequality and graph.

-3x + 12 < 0

Solution :

-3x + 12 < 0

Subtract 12 on both sides

-3x + 12 - 12 < 0 - 12

-3x < -12

Divide by -4 on both sides

-3x/(-3) < -12/(-3)

x < 4

So, any real number less 4 is a solution of the given equation.

The solution set of the given inequality is (-∞, 2].

Example 3 :

Solve the following linear inequality and graph.

4x - 12 ≥  0

Solution :

4x - 12 ≥  0

Add 12 on both sides

4x - 12 + 12  ≥  0 + 12

4x  ≥  12

Divide by 4 on both sides

4x/4 ≥ 12/4

x ≥ 3

So, any real number greater than or equal to 3 is a solution of the given equation.

The solution set of the given inequality is [3, ∞).

Example 4 :

Solve the following linear inequality and graph.

7x + 9 > 30

Solution :

7x + 9 > 30

Subtract 9 on both sides

7x + 9 - 9 > 30 - 9

7x  > 21

Divide by 7 on both sides

7x/7 > 21/7

x > 3

So, any real number greater than 3 is a solution of the given equation.

The solution set of the given inequality is (3, ∞).

Example 5 :

Solve the following linear inequality and graph.

5x - 3 < 3x + 1

Solution :

5x - 3 < 3x + 1

Subtract 3x on both sides

5x - 3 - 3x  < 3x + 1 - 3x 

2x - 3 <  1 

Add 3 on both sides

2x - 3 + 3 <  1 + 3

2x < 4

Divide by 2 on both sides

2x/2 < 4/2

x < 2

So, any real number lesser than 2 is a solution of the given equation.

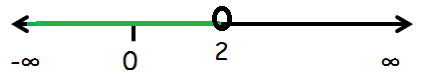
The solution set of the given inequality is (2, ∞).

Example 6 :

Solve the following linear inequality and graph.

3x + 17 ≤ 2(1 - x)

Solution :

3x + 17 ≤ 2(1 - x)

3x + 17 ≤ 2 - 2x

Add 2x on both sides

3x + 2x + 17  ≤ 2 - 2x + 2x

5x + 17 ≤ 2 

Subtract 17 on both sides

5x + 17 - 17 ≤ 2 - 17

5x ≤ -15

Divide by 5 on both sides

5x/5 ≤ -15/5

x ≤ -3

So, any real number lesser than or equal to -3 is a solution of the given equation.

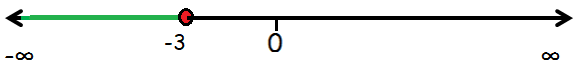
The solution set of the given inequality is (-∞ , -3].

Example 7 :

Solve the following linear inequality and graph.

2(2x + 3) - 10 ≤ 6 (x - 2)

Solution :

2(2x + 3) - 10 ≤ 6 (x - 2)

4x + 6 - 10 ≤ 6 x - 12

4x - 4 ≤ 6 x - 12

Subtract 6x on both sides

4x - 4 - 6x  ≤ 6 x - 12 - 6x 

-2x - 4 ≤ - 12

Add 4 on both sides

-2x - 4 + 4 ≤ - 12 + 4

-2x ≤ - 8

Divide by -2 on both sides

-2x / (-2) ≤ - 8 / (-2)

x ≤ 4

So, any real number lesser than or equal to 4 is a solution of the given equation.

The solution set of the given inequality is (-∞ , 4].

Example 8 :

Elisa won 40 lollipops playing basketball at the school fair. She gave two to every student in her math class. She has at least 7 lollipops left.

a) Write an inequality to represent the situation. Be sure to define your variable.

b) Solve the inequality to find the maximum number of students in her class.

Solution :

Number of lollipops = 40

Number of students in her class = x

a) 

40 - 2x ≥ 7

-2x ≥ 7 - 40

-2x ≥ -33

x ≤ 33/2

x ≤ 16.5

b) Maximum number of students in her class is 16.

Example 9 :

More than 450 students went on a field trip. Ten buses were filled and 5 more students traveled in a car.

a) Write an inequality to represent the situation. Be sure to define your variable.

b) Solve the inequality to find the minimum number of people on each bus.

Solution :

a)  Let x be the number of people in each bus.

10x + 5 > 450

10x > 450 - 5

10x > 445

x > 445/10

x > 44.5

b) The minimum number of people on each bus is 44.

Example 10 :

Bill spent less than $26 on a magazine and five composition books. The magazine cost $4.

a) Write an inequality to represent the situation. Be sure to define your variable.

b) Solve the inequality to find the maximum cost of each composition book.

Solution :

Let x be the cost of each composition book.

Number of magazines he purchases = 1

cost of it = $4

4 + 5x < 26

Subtracting 4

5x < 26 - 4

5x < 22

Dividing by 5, we get

x < 22/5

x < 4.4

So, the maximum cost of each composition book is $4.4.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.