GRAPH TRIANGLES AND QUADRILATERALS

The following steps will be useful to graph triangles and quadrilaterals on the coordinate plane.  

(i)  Mark the given points on the graph sheet one by one.

(x, y)  ==>  Choose the first quadrant

(-x, y)  ==> Choose the second quadrant

(-x, -y)  ==> Choose the third quadrant

(x, -y)  ==> Choose the fourth quadrant

(ii)  Join the marked points.

(iii) Name the vertices.

Example 1 :

Graph the triangle with vertices (2, -3), (-6, -7) and (-8, -3)

Solution :

(2, -3) ===> (x, -y)  ===> lies in the fourth quadrant

(-6, -7)  ===> (-x, -y)  ===> lies in the third quadrant

(-8, -3)  ===> (-x, -y)  ===> lies in the third quadrant

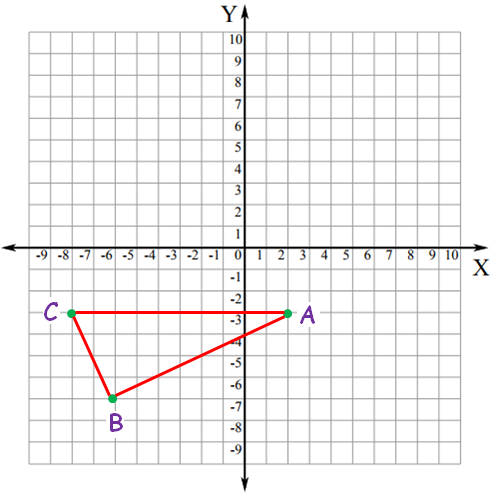
By plotting the given points, we got above triangle ABC.

Example 2 :

Graph the vertices(-7, -5), (-4, 3), (5, 6) and (2, –2) and name the quadrilateral so formed.

Solution :

(-7, -5) ===> (-x, -y)  ===> lies in the third quadrant

(-4, 3)  ===> (-x, y)  ===> lies in the second quadrant

(5, 6)  ===> (x, y)  ===> lies in the first quadrant

(2, -2)  ===> (x, -y)  ===> lies in the fourth quadrant

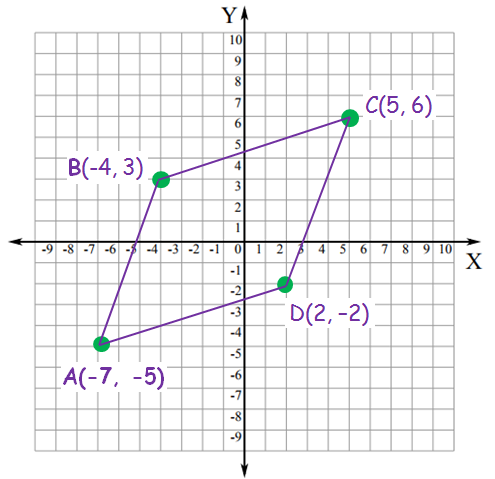
By plotting the given points, we got above parallelogram ABCD. 

So, ABCD is a parallelogram.

Example 3 :

Graph the vertices (0, 0), (3, 4), (0, 8) and (-3, 4) and name the quadrilateral so formed.

Solution :

(0, 0)  ===> Origin 

(3, 4)  ===> (x, y)  ===> lies in the first quadrant

(0, 8)  ===> (0, y)  ===> lies on the y-axis 

(-3, 4)  ===> (-x, y)  ===> lies in the second quadrant

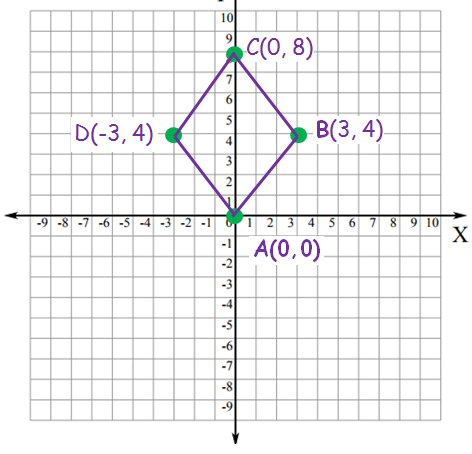
By plotting the given points, we got above rhombus ABCD. 

Hence ABCD is a rhombus.

Example 4 :

Graph the vertices (8, 3), (0, -1), (-2, 3) and (6, 7) and name the quadrilateral so formed.

Solution :

(8, 3)  ===> (x, y) ===> lies in the first quadrant 

(0, -1)  ===> (0, -y) ===> lies on the y-axis

(-2, 3)  ===> (-x, y) ===> lies in the second quadrant

(6, 7)  ===> (x, y)  ===> lies in the first quadrant 

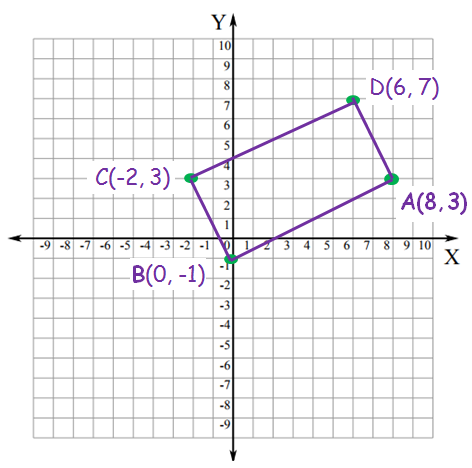
By plotting the given points, we got above rectangle ABCD. 

So, ABCD is a rectangle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.