GRAPHING ABSOLUTE VALUE FUNCTIONS WORKSHEET

Graph the following absolute value functions.

1. y = |x - 1|

2. y = |x - 1| - 2

3. y = |x + 3| + 3

4. y = |x - 2|

5. y = |x + 4| + 3

6. y = |x - 4| - 4

7. y = -|x - 2| - 2

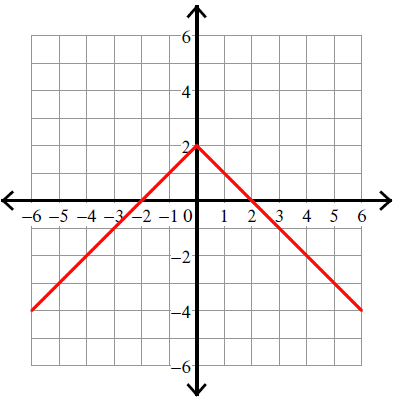
8. y = -|x - 4|

9. y = -|x| + 2

10. y = -|x + 1| + 3

11. y = -|x| + 4

12. y = -|x + 1| - 1

1. Answer :

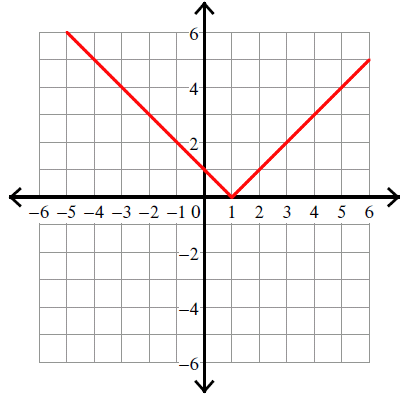
y = |x - 1|

y = |x - 1| ----> y = |x - 1| + 0

Compare :

y = |x - h| + k

y = |x - 1| + 0

Vertex (h, k) = (1, 0).

2. Answer :

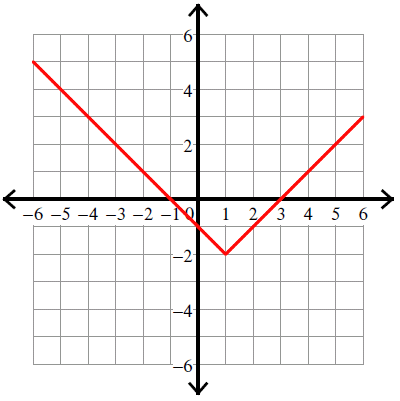
y = |x - 1| - 2

Compare :

y = |x - h| + k

y = |x - 1| - 2

Vertex (h, k) = (1, -2).

3. Answer :

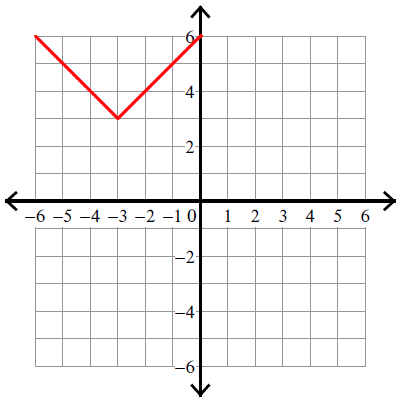
y = |x + 3| + 3

Compare :

y = |x - h| + k

y = |x + 3| + 3

Vertex (h, k) = (-3, 3).

4. Answer :

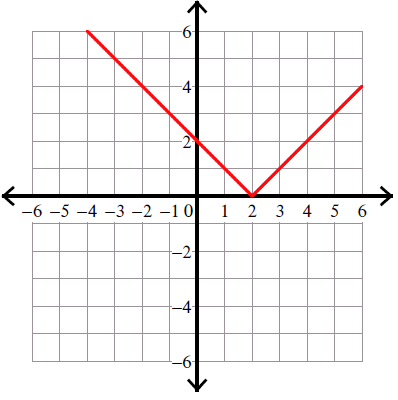
y = |x - 2|

y = |x - 2| ----> y = |x - 2| + 0

Compare :

y = |x - h| + k

y = |x - 2| + 0

Vertex (h, k) = (2, 0).

5. Answer :

y = |x + 4| + 3

Compare :

y = |x - h| + k

y = |x + 4| + 3

Vertex (h, k) = (-4, 3).

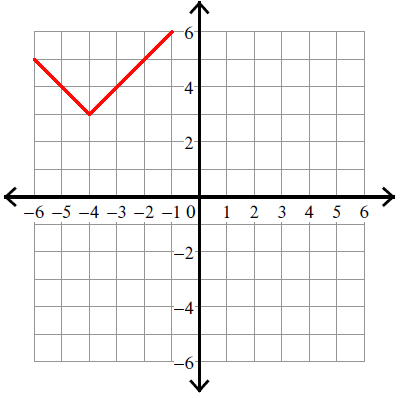
6. Answer :

y = |x - 4| - 4

Compare :

y = |x - h| + k

y = |x - 4| - 4

Vertex (h, k) = (4, -4).

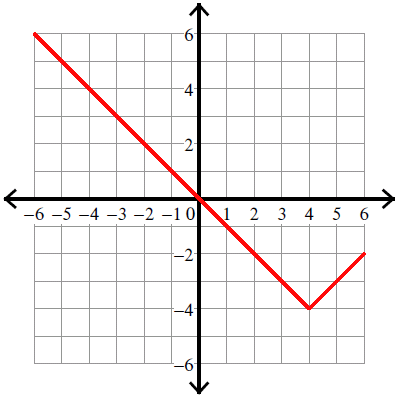
7. Answer :

y = -|x - 2| - 2

Compare :

y = |x - h| + k

y = -|x - 2| - 2

Vertex (h, k) = (2, -2).

Because there is negative sign in front of the absolute sign, we have to flip the curve over.  

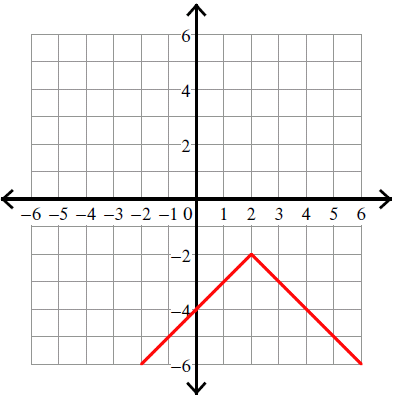
8. Answer :

y = -|x - 4|

y = -|x - 4| ----> y = -|x - 4| + 0

Compare :

y = |x - h| + k

y = -|x - 4| + 0

Vertex (h, k) = (4, 0).

Because there is negative sign in front of the absolute sign, we have to flip the curve over. 

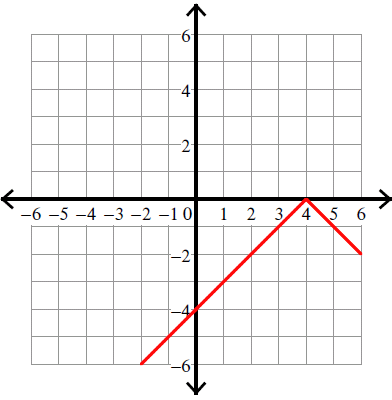
9. Answer :

y = -|x| + 2

y = -|x| + 2 ----> y = -|x - 0| + 2

Compare :

y = |x - h| + k

y = -|x - 0| + 2

Vertex (h, k) = (0, 2).

Because there is negative sign in front of the absolute sign, we have to flip the curve over.  

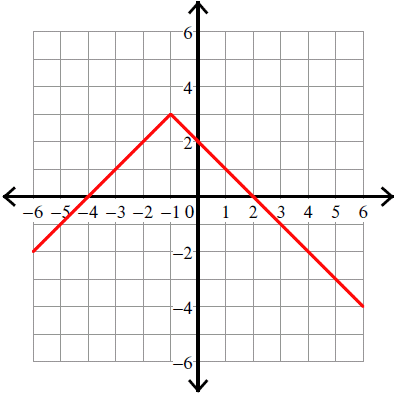
10. Answer :

y = -|x + 1| + 3

Compare :

y = |x - h| + k

y = -|x + 1| + 3

Vertex (h, k) = (-1, 3).

Because there is negative sign in front of the absolute sign, we have to flip the curve over. 

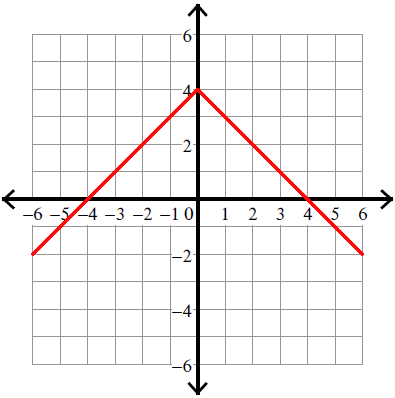
11. Answer :

y = -|x| + 4

y = -|x| + 4 ----> y = -|x - 0| + 4

Compare :

y = |x - h| + k

y = -|x - 0| + 4

Vertex (h, k) = (0, 4).

Because there is negative sign in front of the absolute sign, we have to flip the curve over. 

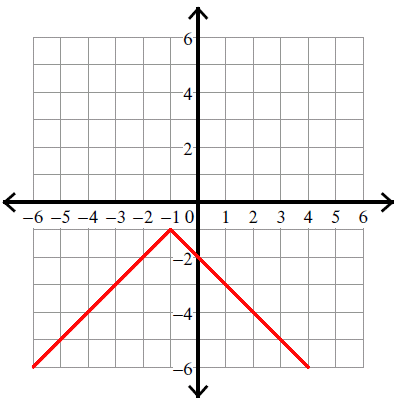
12. Answer :

y = -|x + 1| - 1

Compare :

y = |x - h| + k

y = -|x + 1| - 1

Vertex (h, k) = (-1, -1).

Because there is negative sign in front of the absolute sign, we have to flip the curve over.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.