GRAPHING GREATEST INTEGER FUNCTION

The greatest integer function is denoted by

y = [x]

For all real values of x, the greatest integer function returns the greatest integer which is less than or equal to x.

To graph the parent function y = [x], we have to substitute some random values for x.

Substitute x = -3, -2, -1, 0, 1, 2, 3.

y = [-3] = -3 ----> (-3, -3)

y = [-2] = -2 ----> (-2, -2)

y = [-1] = -1 ----> (-1, -1)

y = [0] = 0 ----> (0, 0)

y = [1] = 1 ----> (1, 1)

y = [2] = 2 ----> (2, 2)

y = [3] = 3 ----> (3, 3)

How to plot the above points on the graph?

Let us take the point (-3, -3).

Mark the point on xy- plane with a filled circle at (-3, -3).

Then extend a line for 1 space on the left side of (-3, -3) and end up with empty circle.

Do the same thing for the other points too.

Now you will have a graph as given below.

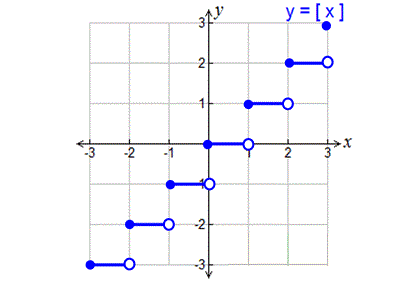
Graphing Greatest Integer Function - Steps

Example 1 :

Graph : y = [x - 2].

Solution :

The given function is in the form of y - a = [x - b].

Let y = 0 and x - 2 = 0. Then, y = 0 and x = 2.

From y = 0, there is no vertical shift.

From x = 2, we have an horizontal shift of 2 units to the right.

So each point of the parent function to be shifted 2 units to the right.

If we do the above transformation, we will have a graph as given below.

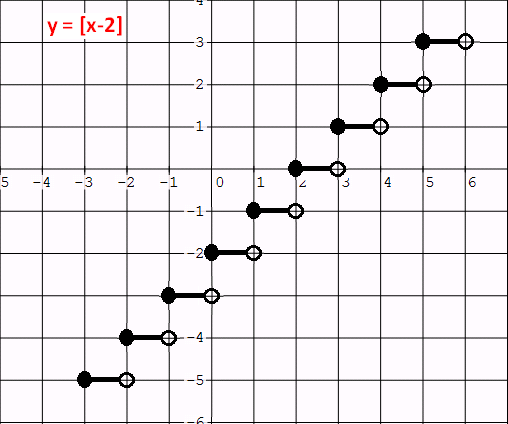
Example 2 :

Graph : y = [x] + 3.

Solution :

If we write the given function in the form of

y - a = [x - b],

we will have y - 3 = [x].

Let y - 3 = 0 and x = 0. Then, y = 3 and x = 2.

From y = 3, we have a vertical shift of 3 units up.

From x = 0, there is no horizontal shift.

So each point of the parent function to be shifted 3 units up.

If we do the above transformation, we will have a graph as given below.

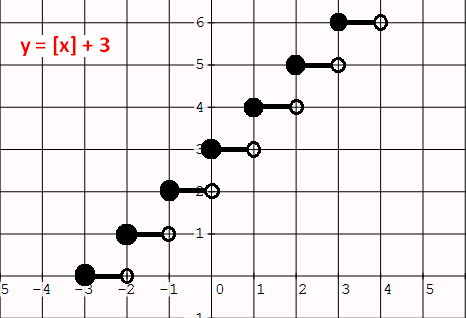
Example 3 :

Graph : y = [x + 1] + 2.

Solution :

If we write the given function in the form of

y - a = [x - b],

we will have y - 2 = [x + 1].

Let y - 2 = 0 and x + 1 = 0. Then y = 2 and x = -1.

From y = 2, we have a vertical shift of 2 units up.

From x = - 1, we have an horizontal shift of 1 unit to the left.

So each point of the parent function to be shifted 2 units up and 1 unit to the left.

If we do the above transformations, we will have a graph as given below.

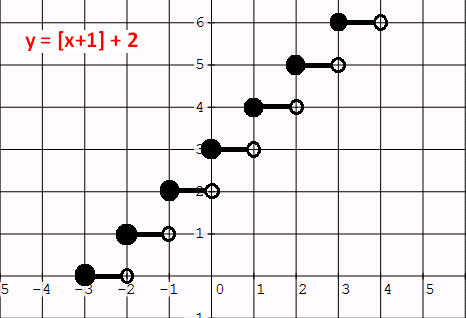
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.