GRAPHING LINEAR EQUATIONS IN SLOPE INTERCEPT FORM WORKSHEET

Graph the following linear equations.

Problem 1 :

y = -x + 5

Problem 2 :

y = 2x

Problem 3 :

9x + 4y = 16

Problem 4 :

3x - 2y + 4 = 0

Problem 5 :

2x - 3y = 9

Problem 6 :

y = 4

Problem 7 :

x = -4

Answers

1. Answer :

y = -x + 5

The above linear equation is in slope-intercept form.

Comparing y = mx + b and y = -x + 5,

slope m = -1

b = 5

Because slope (-1) is a negative value, the line will be a falling line.

rise/run = -1

rise/run = ⁻¹⁄₁

rise = -1

run = 1

Because the y-intercept is 5, the line will intersect y-axis at 5. 

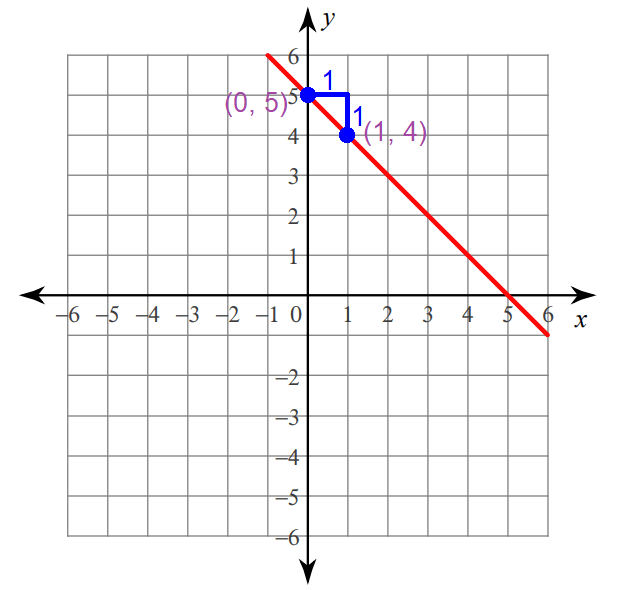
Graphing : 

Step 1 :

Plot the y-intercept at (0, 5). 

Step 2 :

Because the run is 1, move 1 unit to the right from (0, 5).

Step 3 :

Because the rise is -1, move 1 unit down from the position reached in step 2.   

Now, you are at (1, 4). 

Connect the points (0, 5) and (1, 4) to get the line.

2. Answer :

y = 2x

The above linear equation is in slope-intercept form.

Comparing y = mx + b and y = 2x + 0,

slope m = 2

b = 0

Because slope (2) is a positive value, the line will be a rising line.

rise/run = 2

rise/run = ²⁄₁

rise = 2

run = 1

Because the y-intercept is 0, the line will pass through the origin. 

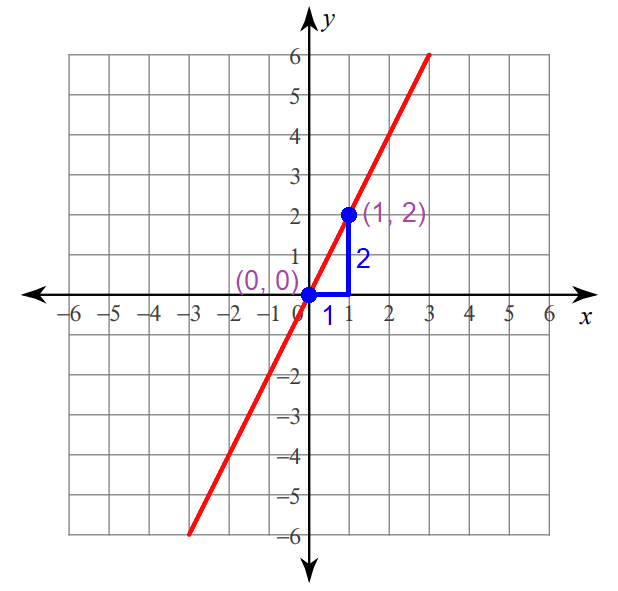
Graphing : 

Step 1 :

Plot the y-intercept at (0, 0). 

Step 2 :

Because the run is 1, move 1 unit to the right from (0, 0).

Step 3 :

Because the rise is 2, move 2 units up from the position reached in step 2.   

Now, you are at (1, 2). 

Connect the points (0, 0) and (1, 2) to get the line.

3. Answer :

9x + 4y = 16

The linear equation above is not in slope-intercept form.

Write it in slope-intercept form.

9x + 4y = 16

Subtract 9x from both sides.

4y = -9x + 16

Divide both sides by 4.

4y = -9x + 16

⁴ʸ⁄₄ = ⁽⁻⁹ˣ ⁺ ¹⁶⁾⁄₄

y = ⁻⁹ˣ⁄₄ ⁺ ¹⁶⁄₄

y = (⁻⁹⁄₄)x + 4

Comparing y = mx + b and y = (⁻⁹⁄₄)x + 4,

slope m = ⁻⁹⁄₄

b = 4

Because slope (⁻⁹⁄₄) is a negative value, the line will be a falling line.

rise/run = ⁻⁹⁄₄

rise = -9

run = 4

Because the y-intercept is 4, the line will intersect y-axis at 4. 

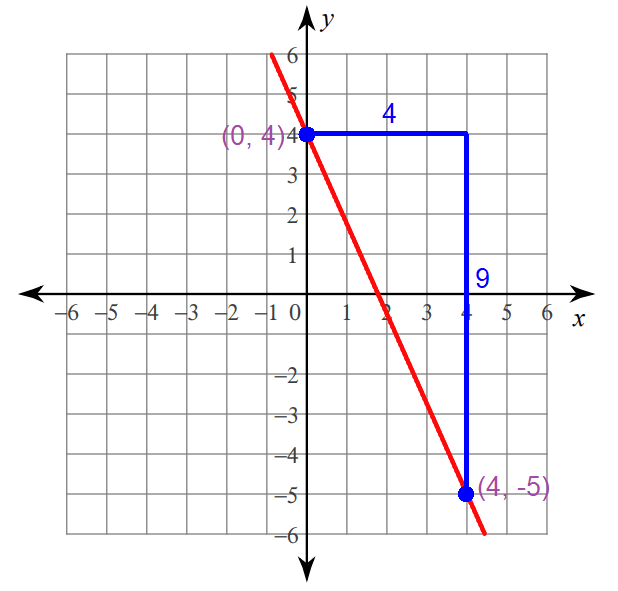
Graphing : 

Step 1 :

Plot the y-intercept at (0, 4). 

Step 2 :

Because the run is 4, move 4 units to the right from (0, 4).

Step 3 :

Because the rise is -9, move 9 units down from the position reached in step 2.   

Now, you are at (4, -5). 

Connect the points (0, 4) and (4, -5) to get the line.

4. Answer :

3x - 2y + 4 = 0

The linear equation above is not in slope-intercept form.

Write it in slope-intercept form.

3x - 2y + 4 = 0

Add 2y to both sides.

3x + 4 = 2y

2y = 3x + 4

Divide both sides by 2.

²ʸ⁄₂ = ⁽³ˣ ⁺ ⁴⁾⁄₂

y = ³ˣ⁄₂ ⁺ ⁴⁄₂

y = (³⁄₂)x + 2

Comparing y = mx + b and y = (³⁄₂)x + 2,

slope m = ³⁄₂

b = 2

Because slope (³⁄₂) is a positive value, the line will be a rising line.

rise/run = ³⁄₂

rise = 3

run = 2

Because the y-intercept is 2, the line will intersect y-axis at 2. 

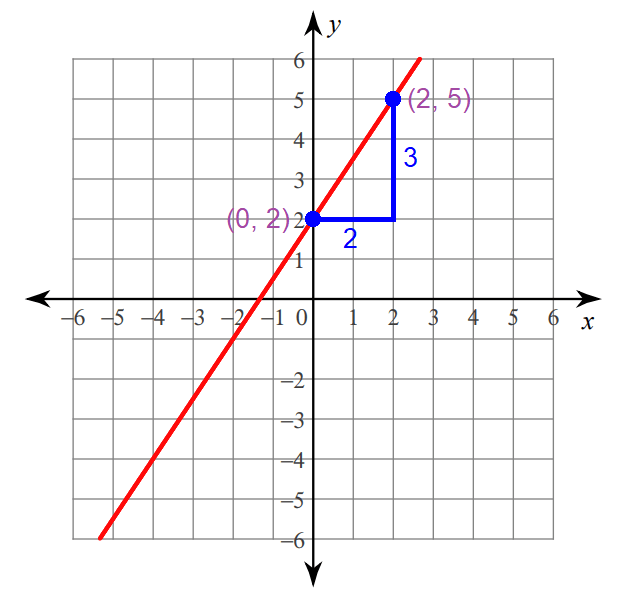
Graphing : 

Step 1 :

Plot the y-intercept at (0, 2). 

Step 2 :

Because the run is 2, move 2 units to the right from (0, 2).

Step 3 :

Because the rise is 3, move 3 units up from the position reached in step 2.   

Now, you are at (2, 5). 

Connect the points (0, 2) and (2, 5) to get the line.

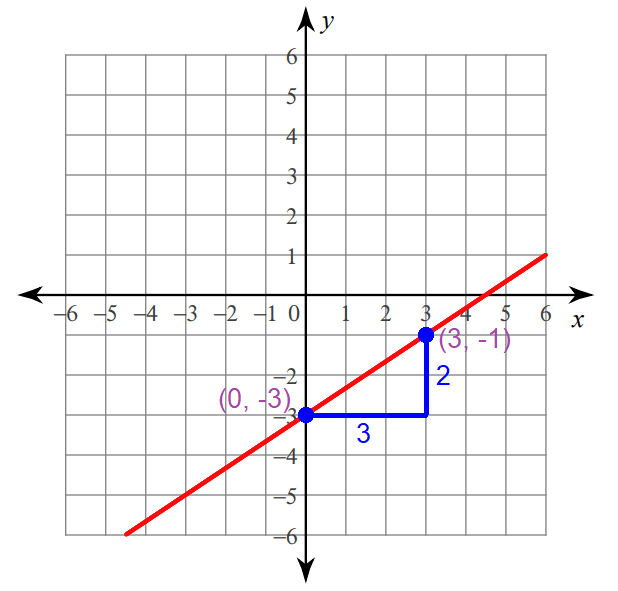
5. Answer :

2x - 3y = 9

The linear equation above is not in slope-intercept form.

Write it in slope-intercept form.

2x - 3y = 9

Add 3y to both sides.

2x = 3y + 9

Subtract 9 from both sides.

2x - 9 = 3y

3y = 2x - 9

Divide both sides by 3.

³ʸ⁄₃ = ⁽²ˣ ⁻ ⁹⁾⁄₃

y = ²ˣ⁄₃ ⁻ ⁹⁄₃

y = ²ˣ⁄₃ - 3

Comparing y = mx + b and y = ²ˣ⁄₃ - 3,

slope m = ²⁄₃

b = -3

Because slope (²⁄₃) is a positive value, the line will be a rising line.

rise/run = ²⁄₃

rise = 2

run = 3

Because the y-intercept is -3, the line will intersect y-axis at -3. 

Graphing : 

Step 1 :

Plot the y-intercept at (0, -3). 

Step 2 :

Because the run is 3, move 3 units to the right from (0, -3).

Step 3 :

Because the rise is 2, move 2 units up from the position reached in step 2.   

Now, you are at (3, -1). 

Connect the points (0, -3) and (3, -1) to get the line.

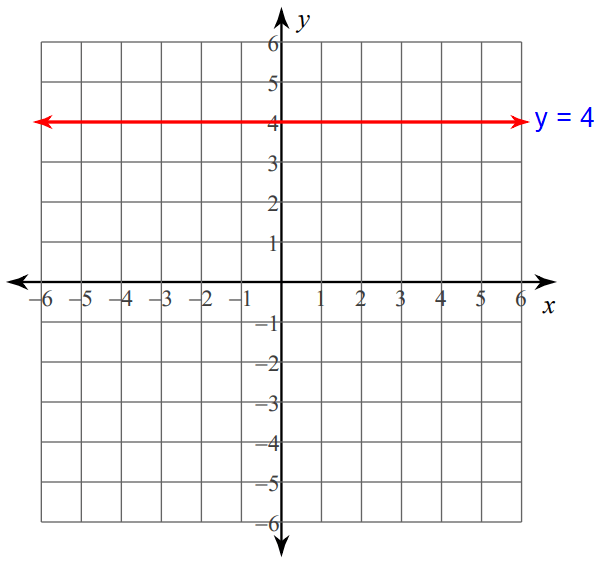
6. Answer :

The graph of a linear equation in one variable will either be an horizontal line or a vertical line.

The linear equation y = 4 contains only one variable, that is y.

Because y = 4 contains the variable y, its graph is an horizontal line through the value 4 on y-axis.

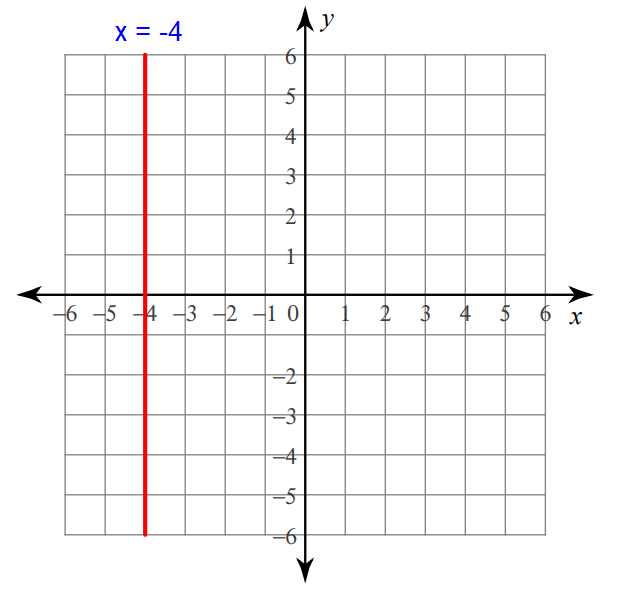
7. Answer :

The linear equation x = -4 contains only one variable, that is x.

Because x = -4 contains the variable x, its graph is a vertical line through the value -4 on x-axis.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.