GRAPHING LINEAR EQUATIONS USING INTERCEPTS WORKSHEET

Use intercepts to graph the line described by each  equation.

Problem 1 : 

x + y  =  -2

Problem 2 : 

x - y  =  1

Problem 3 : 

x + 2y  =  4

Problem 4 : 

y  =  x + 3

Problem 5 : 

y  =  -x + 5

Problem 6 :

y  =  0.5x - 3

Problem 7 :

If the x-intercept of a line is positive and the y-intercept is negative, does the line slant upward or downward from left to right ? Explain your reasoning.

Problem 8 :

A student says that the x-intercept and y-intercept of the graph x + 2y = 5 are the points (0, 5) and (5/2, 0) respectively, why is the student is incorrect?

Problem 9 :

The function below shows the cost to attend the fair if you ride r rides.

f(r) = 5 + 1.75r

a. What is the y-intercept, and what does it mean?

b. What is the slope, and what does it mean?

c. If Al spent $19.00 at the fair, how many rides did Al ride?

Problem 10 :

A band is performing at an auditorium for a fee of $1500. In addition to this fee, the band receives 30% of each $20 ticket sold. The maximum capacity of the auditorium is 800 people.

a. Write an equation that represents the band’s revenue R when x tickets are sold.

b. The band needs $5000 for new equipment.

How many tickets must be sold for the band to earn enough money to buy the new equipment?

Detailed Answer Key

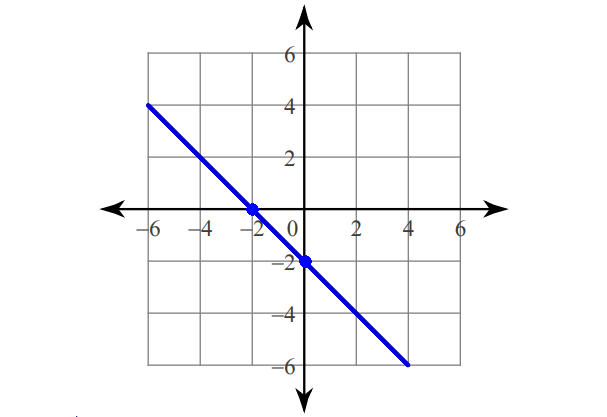
1. Answer : 

Find the intercepts.

Plot (-2, 0) and (0, -2).

Connect with a straight line.

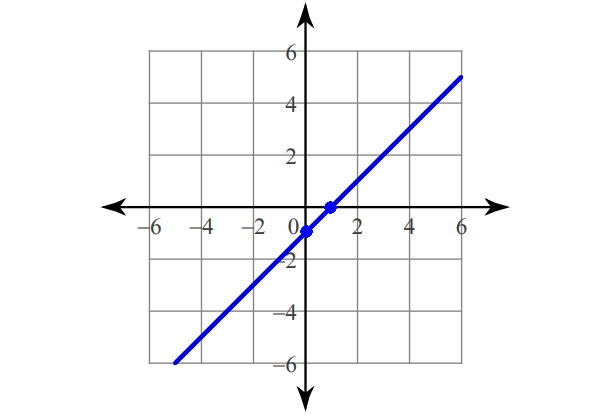
2. Answer : 

Find the intercepts.

Plot (1, 0) and (0, -1).

Connect with a straight line.

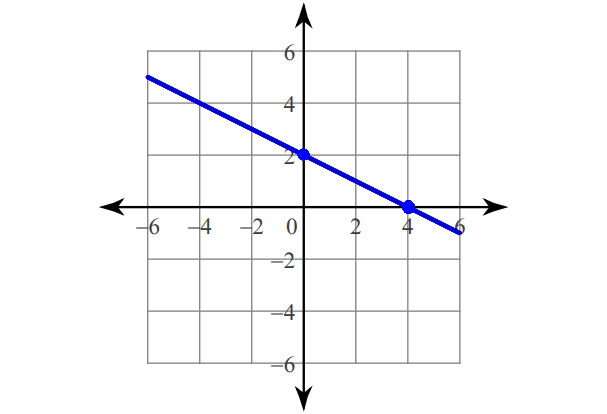
3. Answer : 

Find the intercepts.

Plot (4, 0) and (0, 2).

Connect with a straight line.

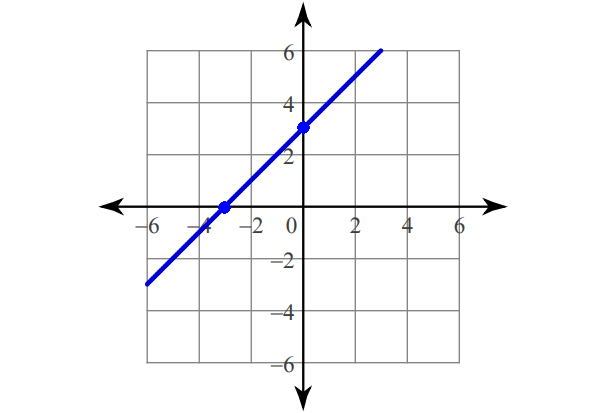
4. Answer : 

Find the intercepts.

Plot (-3, 0) and (0, 3).

Connect with a straight line.

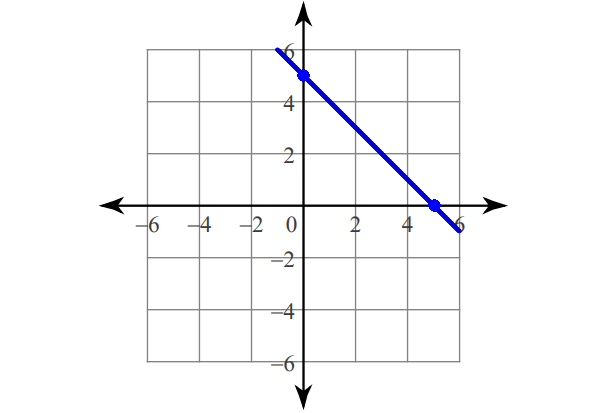
5. Answer : 

Find the intercepts.

Plot (5, 0) and (0, 5).

Connect with a straight line.

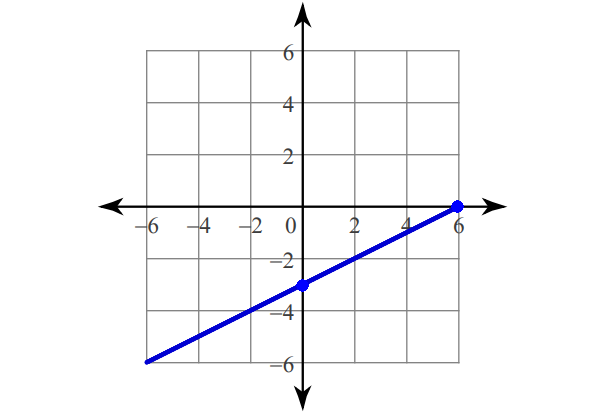
6. Answer : 

Find the intercepts.

Plot (6, 0) and (0, -3).

Connect with a straight line.

7. Answer : 

Given information says, the sign of x-intercept is positive and the sign of y-intercept is negative.

Let us choose two points randomly based on this information.

• x-intercept is at (1, 0)
• y-intercept is at (0, -1)

Finding the slope (m) = (y₂ - y₁) / (x₂ - x₁)

= (-1 - 0) / (0 - 1)

= -1/(-1)

m = 1 (slope is positive)

Then it must be raising line accordingly given terms slant upward line.

8. Answer :

x + 2y = 5 is the point (0, 5)

Finding x-intercept :

Put y = 0

x + 2(0) = 5

x = 5

x-intercept is at (5, 0)

Finding y-intercept :

Put x = 0

0 + 2y = 5

2y = 5

y = 5/2

y-intercept is at (0, 5/2)

Every point will be represented in the form, (x, y)

But in the students answer the answer is completely changed. So, it is incorrect.

9. Answer : 

f(r) = 5 + 1.75r

f(r) - cost spent for ride

r - number of rides

a. Here by comparing the given equation with y = mx + b

y-intercept is at 5. So, the amount to be paid before go to raid is 5.

b. Slope is 1.75

For each number of extra rides, we have to pay 1.75 extra.

c. Here f(r) = 19

19 = 5 + 1.75r

19 - 5 = 1.75 r

1.75r = 14

r = 14/1.75

r = 8

10. Answer :

Admission fee = $1500

Let x be the number of $20 ticket.

Slope or rate of change = 0.30

a) 

Required equation will be,

y = 0.30x + 1500

b. Here y = $5000

5000 = 0.30x + 1500

5000 - 1500 = 0.30x

0.30x = 3500

x = 3500/0.30

x = 11666.66

Approximately 11667 tickets.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.