GRAPHING LINEAR EQUATIONS USING INTERCEPTS
The following steps will be useful to graph a linear equation using intercepts.
Step 1 :
Find the x-intercept by letting y = 0 and solving for x. Use the x-intercept to plot the point where the line crosses the x-axis.
Step 2 :
Find the y-intercept by letting x = 0 and solving for y. Use the y-intercept to plot the point where the line crosses the y-axis.
Step 3 :
Draw a line through the two points.
Use intercepts to graph the line described by each equation.
Example 1 :
2x + 3y = 12
Solution :
Find the intercepts.
x-intercept :
2x + 3y = 12
2x + 3(0) = 12
2x + 0 = 12
2x = 12
2x/2 = 12/2
x = 6
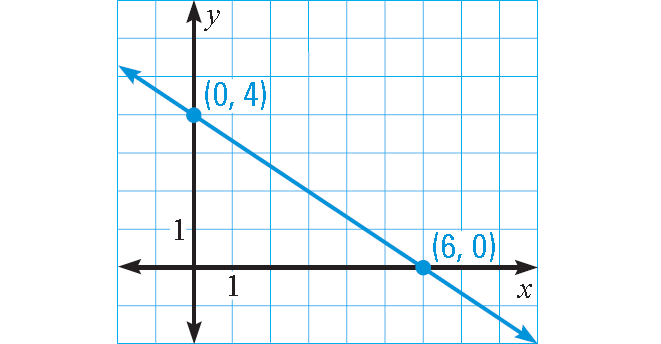
(6, 0)
y-intercept :
2x + 3y = 12
2(0) + 3y = 12
0 + 3y = 12
3y = 12
3y/3 = 12/3
y = 4
(0, 4)
Plot (6, 0) and (0, 4).
Connect with a straight line.
Example 2 :
-2x + 8y = 16
Solution :
Find the intercepts.
x-intercept :
-2x + 8y = 16
-2x + 8(0) = 16
-2x + 0 = 16
-2x = 16
-2x/(-2) = 16/(-2)
x = -8
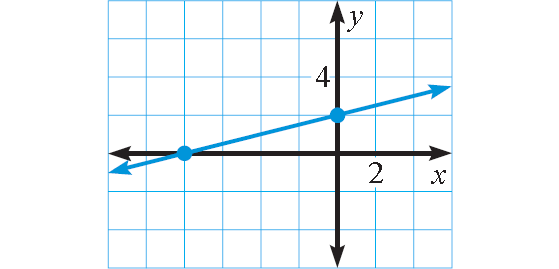
(-8, 0)
y-intercept :
-2x + 8y = 16
-2(0) + 8y = 16
0 + 8y = 16
8y = 16
8y/8 = 16/8
y = 2
(0, 2)
Plot (-8, 0) and (0, 2).
Connect with a straight line.
Example 3 :
y = -0.5x - 1.5
Solution :
Find the intercepts.
x-intercept :
y = -0.5x - 1.5
0 = -0.5x - 1.5
0.5x = -1.5
x = -3
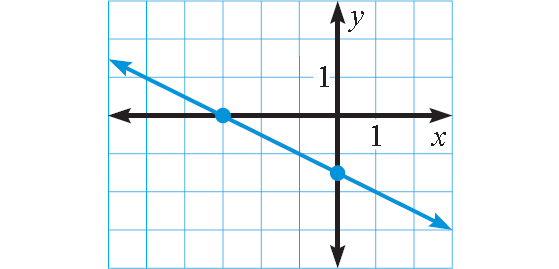
(-3, 0)
y-intercept :
y = -0.5x - 1.5
y = -0.5(0) - 1.5
y = 0 - 1.5
y = -1.5
(0, -1.5)
Plot (-3, 0) and (0, -1.5).
Connect with a straight line.
Example 4 :
y = 2x/3 + 4
Solution :
Find the intercepts.
x-intercept :
y = 2x/3 + 4
0 = 2x/3 + 4
-4 = 2x/3
-12 = 2x
-6 = x
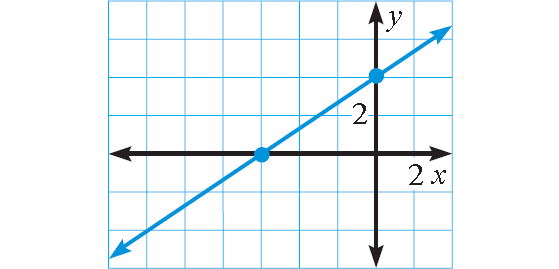
(-6, 0)
y-intercept :
y = 2x/3 + 4
y = 2(0)/3 + 4
y = 0/3 + 4
y = 0 + 4
y = 4
(0, 4)
Plot (-6, 0) and (0, 4).
Connect with a straight line.
Example 5 :
The function below shows the cost of a hamburger with different numbers of toppings (t).
f(t) = 1.90 + 1.40t
a. What is the y-intercept, and what does it mean?
b. What is the slope, and what does it mean?
c. If Jodi paid $3.30 for a hamburger, how many toppings were on Jodi’s hamburger?
Solution :
f(t) = 1.90 + 1.40t
Comparing with the function y = mx + b
f(t) = cost of hamburger
t = different number of toppings
a) y-intercept = 1.90
cost of hamburger with no toping is $1.90
b) Slope = 1.40
Based on number of toppings, the cost of hamburger will increase with the rate of change 1.40.
c) When cost of hamburger = 3.30
3.30 = 1.90 + 1.40x
Subtracting 1.90, we get
3.30 - 1.90 = 1.40x
1.40x = 1.4
x = 1.4/1.40
x = 1
There is 1 toping is added.
Example 6 :
The function below shows the cost of an ice cream sundae with different numbers of toppings (t).
f(t) = 2.25 + 0.75t
a. What is the y-intercept, and what does it mean?
b. What is the slope, and what does it mean?
c. If Kaye paid $6.00 for a sundae, how many toppings were on Kaye’s sundae?
Solution :
f(t) = 2.25 + 0.75t
Comparing with the function y = mx + b
f(t) = cost of ice cream
t = different number of toppings
a) y-intercept = 2.25
cost of ice cream with no toping is $2.25
b) Slope = 0.75
Based on number of toppings, the cost of ice cream will increase with the rate of change 0.75
c) When cost of ice cream = 6.50
6.50 = 2.25 + 0.75t
6.50 - 2.25 = 0.75t
4.25 = 0.75t
t = 4.25 / 0.75
t = 5.6
There is 6 toping is added.
Example 7 :
Colby put $100 in a savings account. The graph below shows how the amount in the account would increase over the next ten years. What does the y-intercept represent?
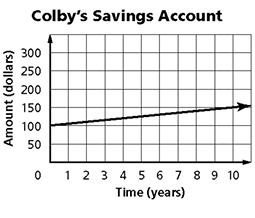
Solution :
Here the y-intercept is $100.
At the beginning, in his bank account he had $100.
Example 8 :
Write the equation of the line in slope-intercept form.
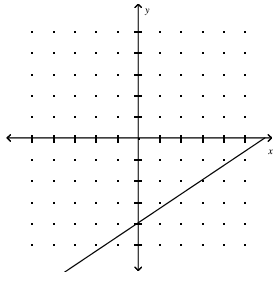
Solution :
From the graph given above, we know that y-intercept = -4
Creating the equation in slope intercept form,
y = mx + b
y = mx - 4
Tracing one more point which lies on the line, we get (3, -2). Applying this point in the equation above
-2 = m(3) - 4
-2 + 4 = 3m
3m = 2
m = 2/3
Applying the slope, we get
y = (2/3)x - 4
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145) -
Digital SAT Math Problems and Solutions (Part - 144)
Apr 14, 25 07:27 PM
Digital SAT Math Problems and Solutions (Part - 144)

