GRAPHING LINEAR NON PROPORTIONAL RELATIONSHIPS USING SLOPE-INTERCEPT FORM
A linear equation is an equation whose solutions are ordered pairs that form a line when graphed on a coordinate plane. Linear equations can be written in the form y = mx + b.
When b ≠ 0, the relationship between x and y is non proportional.
Example :
Ken has a weekly goal of burning 2400 calories by taking brisk walks. The equation y = -300x + 2400 represents the number of calories y Ken has left to burn after x hours of walking which burns 300 calories per hour. After how many hours of walking will Ken have 600 calories left to burn ? After how many hours will he reach his weekly goal?
Solution :
Step 1 :
y = -300x + 2400
The y-intercept is b = 2400. Plot the point that contains the y-intercept : (0, 2400).
Step 2 :
Write the slope as a fraction.
m = -300/1 = -600/2 = -900/3
Using the slope as -900/3 helps in drawing a more accurate graph.
The slope is m = -900/3. Use the slope to find second a point. Since the slope = rise / run, from (0, 2400), count down 900 units and right 3 units.
Then, the new point is (3, 1500).
Step 3 :
Draw a line through the points.
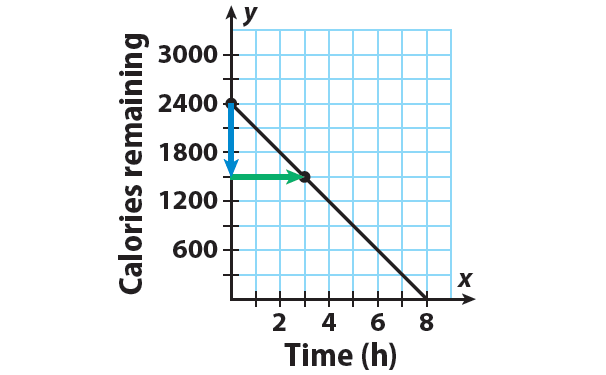
Step 4 :
To find after how many hours of walking will Ken have 600 calories left to burn.
Locate 600 calories on the y-axis. Read across and down to the x-axis.
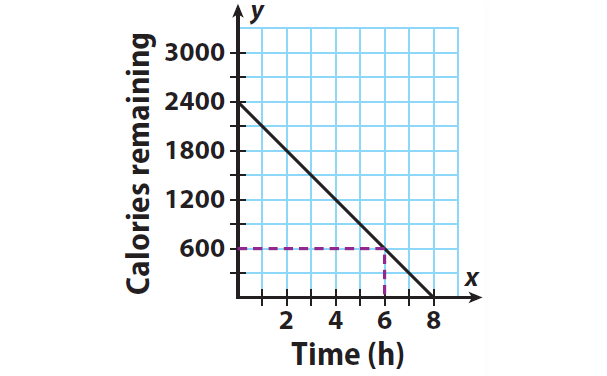
From the graph, we can know that Ken will have 600 calories left to burn after 6 hours.
Step 5 :
Ken will reach his weekly goal when the number of calories left to burn is 0. Because every point on the x-axis has a y-value of 0, find the point where the line crosses the x-axis.
Ken will reach his goal after 8 hours of brisk walking.
Reflect
The relationship between two quantities is linear. How can you conclude from the graph whether the relationship is proportional or non proportional?
If the relationship between the two quantities is linear, its graph will be a line.
If the line goes through the origin, then the relationship is proportional.
If the line does not go through the origin, then the relationship is non proportional.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
