GRAPHING POLAR EQUATIONS r EQUAL TO a COS n THETA IN POLAR GRID

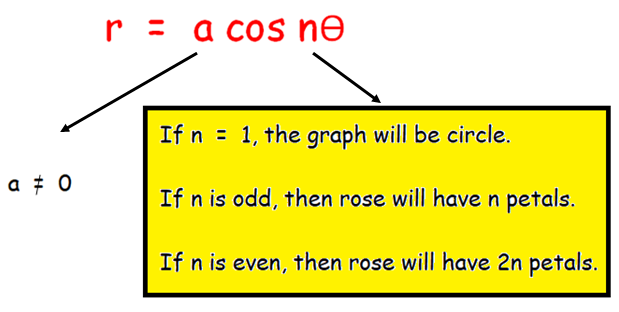
The graph of the polar equation which in the form of 

r  =  a cos nθ

(or)

r  =  a sin nθ

will produce rose curves. They are called rose curves because the loops that are formed by resemble petals.

Maximum r value is |a|.

Note :

If it is cosine function one or more leaves lie on the y axis.

Example 1 :

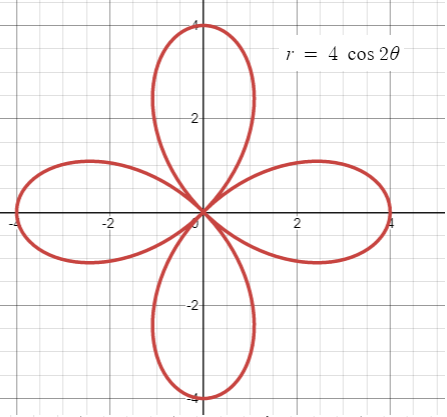
Draw the graph of r  =  4 cos 2θ.

Solution :

a  =  4, n = 2 (even). So the rose curve will have 2n petals.

That is,

2n  =  2(2)  ==>  4 petals

Where will be each petal ?

360 / 4  =  90

Each petal will be apart 90 degree.

The required points are (4, 0) (0, π/2)(-4, π) and (0, 2π).

Example 2 :

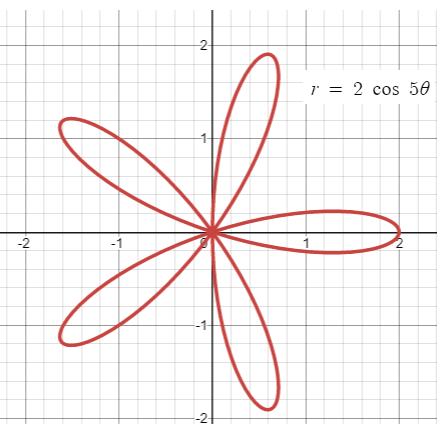
Draw the graph of r  =  2 cos 5θ.

Solution :

a  =  2, n = 5 (odd). So the rose curve will have 5 petals.

Where will be each petal ?

360 / 5  =  72

Each petal will be apart 72 degree.

Since it is cosine function, it will lie on the x - axis based on the value of n.

Example 3 :

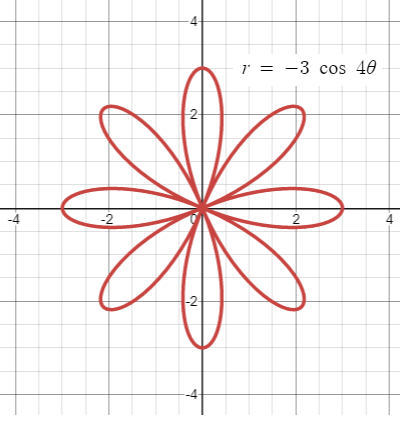
Draw the graph of r  =  -3 cos 4θ.

Solution :

a  =  3, n = 4 (even). So the rose curve will have 2n petals.

That is,

2n  =  2(4)  ==>  8 petals

Where will be each petal ?

360 / 8  =  45

Each petal will be apart 45 degree.

Since it is cosine function, it will lie on the x - axis based on the value of n.

So the positions of petals are 0, 45, 90, 135, 180, 225, 270, 315, 360.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.