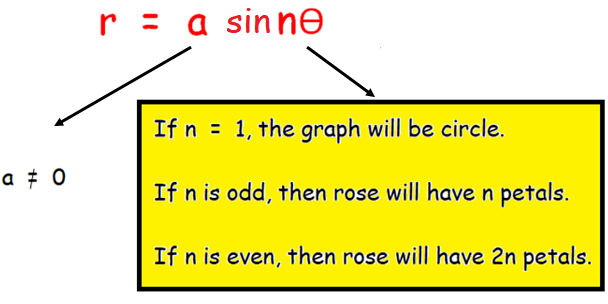
GRAPHING r EQUAL TO A SIN n THETA

The graph of the polar equation which in the form of 

r  =  a sin nθ

(Or)

r  =  a cos nθ

will produce rose curves. They are called rose curves because the loops that are formed by resemble petals.

Maximum r value is |a|.

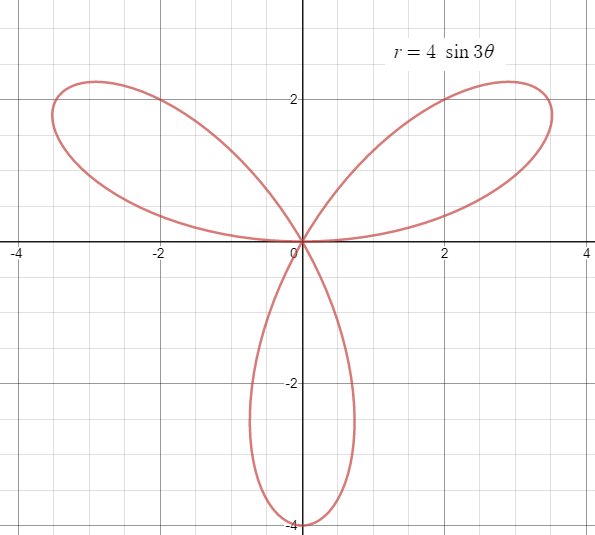
Example 1 :

Draw the graph of r  =  4 sin 3θ.

Solution :

a  =  4, n = 3 (odd). So the rose curve will have n petals.

That is,

3 petals

Where will be each petal ?

360 / 3  =  120

Example 2 :

Analyzing the polar relation  r  =  5 sin 3θ

(a)  Type of curve

(b)  Algebraically find the values of θ where the tips of the petals occur for 0 ≤ θ ≤ 2π 

(c)  Graph r  =  5 sin 3θ over 0 ≤ θ ≤ 2π, using petals tips as guide. Identify the starting point use arrows to indicate the directions of motion and find the number of petals accordingly.

(d)  Find the zeroes of r for 0 ≤ θ ≤ 2π.

Solution :

(a)  Since the value of n is more than 1, it will give rose curves.

(b)

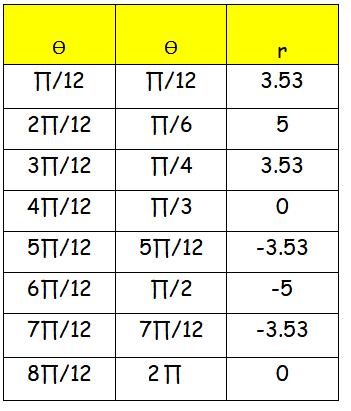
Like this by applying some more values, we will get another rose petal and that will lie on y axis.

(c)

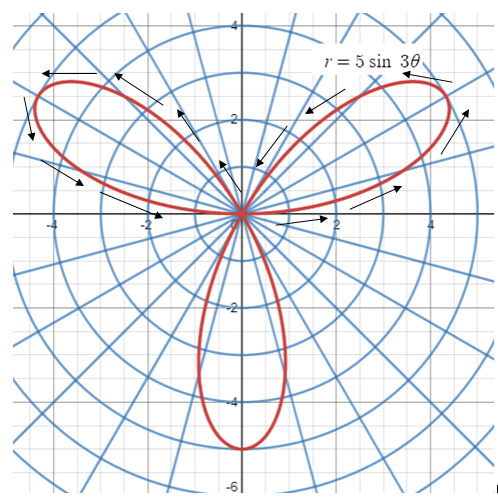
Total number of petals is 3.

(d)  r  =  5 sin 3θ

Zeroes of r :

5 sin 3θ  =  0

sin 3θ  =  0

3θ  =  sin^-1(0)

3θ  =  0, ∏, 2∏, 3∏,.......

θ  = n∏/3 and n ∈ Z (integer)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.