GRAPHING ROTATIONS WORKSHEET

Problem 1 :

The triangle XYZ has the following vertices X(0, 0), Y(2, 0) and Z(2, 4). Rotate the triangle XYZ 90° counterclockwise about the origin.

Problem 2 :

The triangle PQR has the following vertices P(0, 0), Q(-2, 3) and R(2,3). Rotate the triangle PQR 90° clockwise about the origin.

Problem 3 :

A quadrilateral has the following vertices A(0, 0), B(1, 2), C(4, 2) and D(3, 0). Rotate the quadrilateral 180° clockwise about the origin.

Problem 4 :

The triangle XYZ has the following vertices X(0, 0), Y(2, 0) and Z(2, 4). Rotate the triangle XYZ 270° counterclockwise about the origin.

1. Answer :

Step 1 :

Trace triangle XYZ and the x- and y-axes onto a piece of paper.

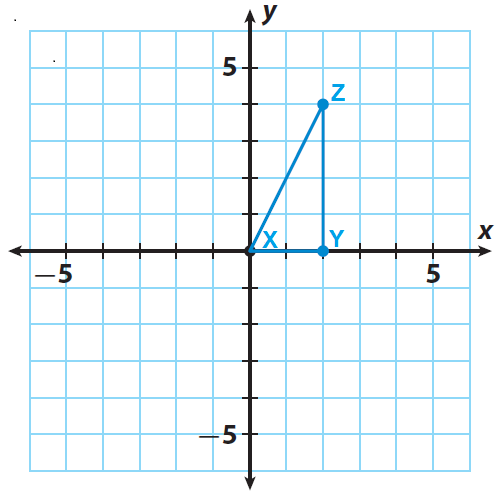
Step 2 :

Let X', Y' and Z' be the vertices of the rotated figure.

Since the triangle is rotated 90° counterclockwise about the origin, the rule is

(x, y) ----> (-y, x)

Step 3 :

X(0, 0) ----> X'(0, 0)

Y(2, 0) ----> Y'(0, 2)

Z(2, 4) ----> Z'(-4, 2)

Step 4 :

Sketch the image X'Y'Z' using the points X'(0, 0),  Y'(0, 2) and  Z'(-4, 2).

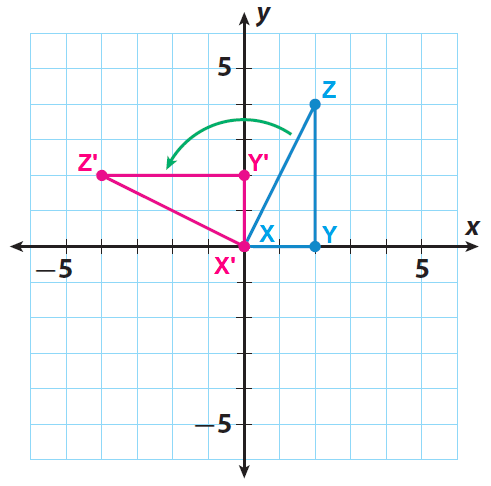
2. Answer :

Step 1 :

Trace triangle PQR and the x- and y-axes onto a piece of paper.

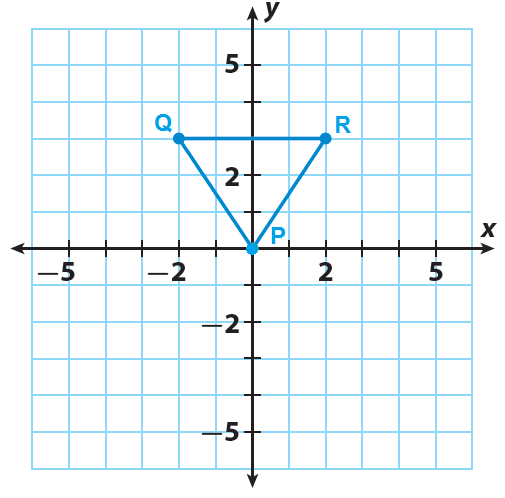
Step 2 :

Let P', Q' and R' be the vertices of the rotated figure.

Since the triangle is rotated 90° clockwise about the origin, the rule is

(x, y) ----> (y, -x)

Step 3 :

P(0, 0) ----> P'(0, 0)

Q(-2, 3) ----> Q'(3, 2)

R(2, 3) ----> R'(3, -2)

Step 4 :

Sketch the image P'Q'R' using the points P'(0, 0),  Q'(3, 2) and  Z'(3, -2).

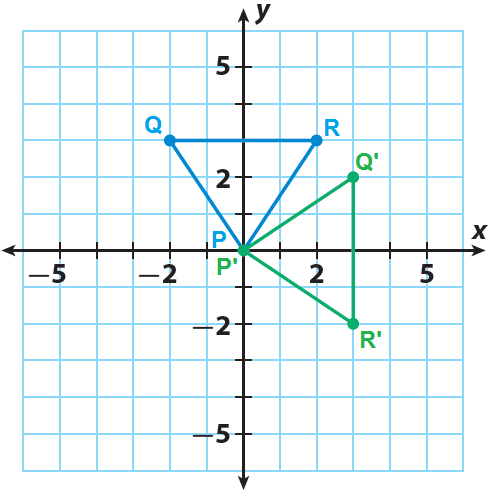
3. Answer :

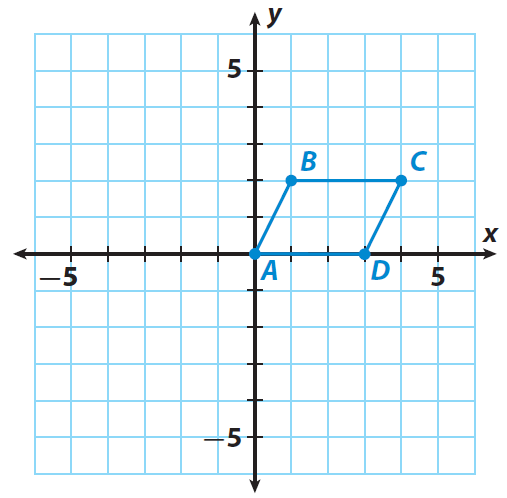
Step 1 :

Trace the quadrilateral ABCD and the x- and y-axes onto a piece of paper.

Step 2 :

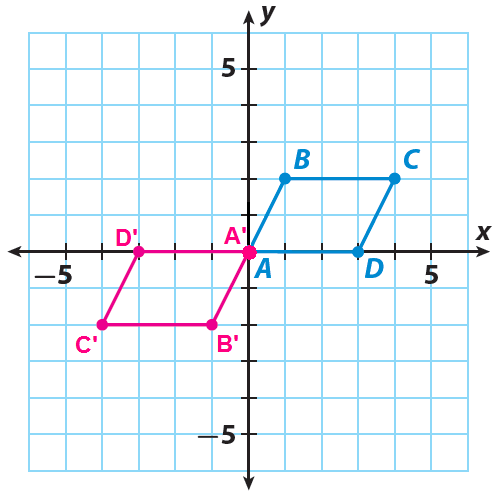
Let A', B', C' and D' be the vertices of the rotated figure.

Since the quadrilateral is rotated 180° clockwise about the origin, the rule is

(x, y) ----> (-x, -y)

Step 3 :

A(0, 0) ----> A'(0, 0)

B(1, 2) ----> B'(-1, -2)

C(4, 2) ----> C'(-4, -2)

D(3, 0) ----> D'(-3, 0)

Step 4 :

Sketch the image A'B'C'D' using the points A'(0, 0), B'(-1, -2), C(-4, -2) and  D'(-3, 0).

4. Answer :

Step 1 :

Trace triangle XYZ and the x- and y-axes onto a piece of paper.

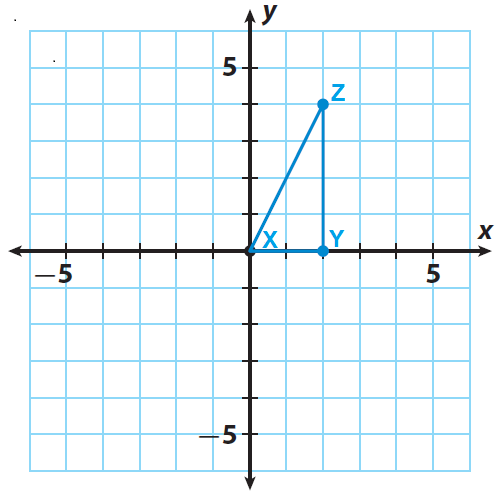
Step 2 :

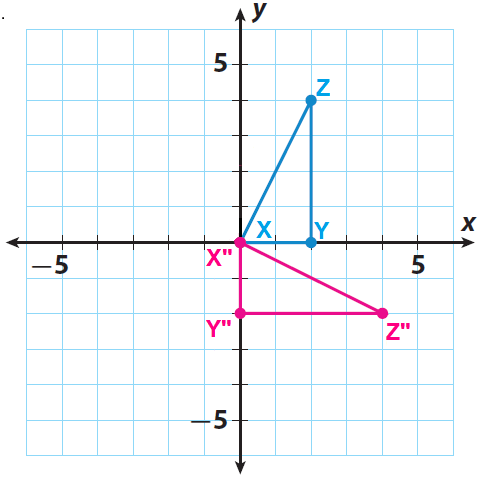
Let X", Y" and Z" be the vertices of the rotated figure.

Since the triangle is rotated 270° counterclockwise about the origin, the rule is

(x, y) ----> (y, -x)

Step 3 :

X(0, 0) ----> X"(0, 0)

Y(2, 0) ----> Y"(0, -2)

Z(2, 4) ----> Z"(4, -2)

Step 4 :

Sketch the image X"Y"Z" using the points X"(0, 0),  Y"(0, -2) and  Z"(4, -2).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.