HARDEST SAT MATH QUESTIONS (Part - 7)

Question 1 :

g(x) = ax² + 24

For the function g defined above, a is a constant and g(4) = 8. What is the value of g(-4) ?

(A) 8             (B) 0             (C) -1             (D) -8

Answer : 

Using the information given, first, we have to find the value of the 'a' in g(x) = ax² + 24. 

g(4)  =  8

ax² + 24  =  8

a(4)² + 24  =  8

16a + 24  =  8

16a  =  -16

a  =  -1

g(x) = -1x² + 24

g(-4) = -1(-4)² + 24

=  -1(16) + 24

=  -16 + 24

=  8

The correct answer is (A). 

Question 2 : 

If x > 3, which of the following is equivalent to

1 / [1/(x + 2) + 1/(x + 3)]

(A)  (2x + 5)/(x² + 5x + 6)

(B)  (x² + 5x + 6)/(2x + 5)

(C)  2x + 5

(D)  x² + 5x + 6

Answer : 

Add 1/(x + 2) and 1/(x + 3). 

1/(x + 2) + 1/(x + 3)  =  [(x + 2) + (x + 3)]/[(x + 2)(x + 3)]

=  (2x + 5)/(x² + 5x + 6)

Then,

1 / [1/(x + 2) + 1/(x + 3)]  =  1 / [(2x + 5)/(x² + 5x + 6)]

=  1 ⋅ [(x² + 5x + 6)/(2x + 5)]

=  (x² + 5x + 6)/(2x + 5)

The correct answer is (B). 

Question 3 : 

If (ax + 2)(bx + 7) = 15x² + cx + 14 for all values of x, and a + b = 8, what are the two possible values for c ?

A) 3 and 5

B) 6 and 35

C) 10 and 21

D) 31 and 41

Answer : .

(ax + 2)(bx + 7)  =  15x² + cx + 14

abx² + 7ax + 2bx + 14  =  15x² + cx + 14

abx² + (7a + 2b)x + 14  =  15x² + cx + 14

Equate the coefficients of x² and x. 

ab  =  15

7a + 2b  =  c ----(1)

It is given that a + b = 8. 

We have to find the values of a and b such that

a + b = 8  and  ab = 15

Possible options are : 

a = 3 and b = 5

a = 5 and b = 3

The correct answer is (D). 

Question 4 : 

If 3x - y = 12, what is the value of 8^x/2^y ?

(A)  2¹²

(B)  4⁴

(C)  8²

(D) The value cannot be determined from the information given.

Answer : .

8^x/2^y  =  (2³)^x/2^y

=  2^3x/2^y

=  2^{3x - y}

Substitute 3x - y = 12.

=  2¹²

The correct answer is (A). 

Question 5 : 

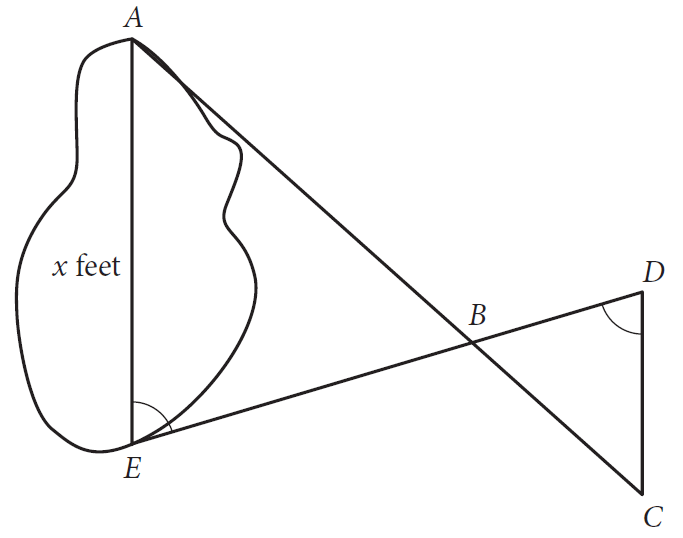
A summer camp counselor wants to find a length, x, in feet, across a lake as represented in the sketch above. The lengths represented by AB, EB, BD, and CD on the sketch were determined to be 1800 feet, 1400 feet, 700 feet, and 800 feet, respectively. Segments AC and DE intersect at B, and ∠AEB and ∠CDB have the same measure. What is the value of x ?

Answer : 

In ΔAEB and ΔCDE, 

m∠AEB  =  m∠CDB (given)

m∠ABE  =  m∠CBD (vertical angles)

By AA Similarity Postulate, ΔAEB and ΔCDE are similar.

So, the corresponding sides are proportional. 

AE/CD  =  BE/BD

Substitute AE = x, BE = 1400, BD = 700 and CD = 800.

x/800  =  1400/700

x/800  =  1400/700

x/800  =  2

Multiply each side by 800.

x  =  1600

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.