HARMONIC MEAN

Harmonic mean is one of the measures of central tendency which can be defined as follows.

For a given set of non-zero observations, harmonic mean is defined as the reciprocal of the arithmetic mean of the reciprocals of the observation.

Let the  variable x assume n values  as given below.

x₁, x₂, x₃, ............x_n

All the above values are being non zero values, then the harmonic mean of x is given by

H = n/∑(1/x_i)

For a grouped frequency distribution, we have

H = N/∑(f_i/x_i)

Properties of Harmonic Mean

1. If all the observations taken by a variable are constants, say k, then the HM of the observations is also k.

2. If there are two groups with n₁ and n₂ observations and H₁ and H₂ as respective HM’s than the combined HM is given by

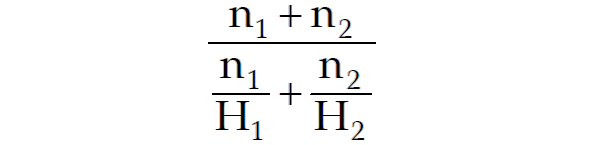
3. Like arithmetic mean, harmonic mean also possess some mathematical properties.

4. It is rigidly defined.

5. It is based on all the observations.

6. It is difficult to comprehend.

7. It is difficult to compute.

8. It has limited applications for the computation of average rates and ratios and such like things. 

Practice Problems

Problem 1 :

Find the harmonic mean for 4, 6 and 10.

Solution :

Formula to find harmonic mean :

H = n/∑(1/x_i)

Fitting the given data in to the above formula, we get

H = 3/(1/4 + 1/6 + 1/10)

= 3/(0.25 + 0.17 + 0.10)

= 5.77

Problem 2 : 

Find the harmonic mean of the first three multiples of 5.

Solution :

The first three multiples of 5 are 5, 10 and 15.

Formula to find harmonic mean :

H = n/∑(1/x_i)

Fitting the given data in to the above formula, we get

H = 3/(1/5 + 1/10 + 1/15)

= 3/(0.25 + 0.17 + 0.10)

= 3/(0.2 + 0.1 + 0.07)

= 3/0.37

= 8.11

Problem 3 :

Find the HM for the following distribution:

x      :      2      4      8      16

f       :      2      3      3      2

Solution : 

Formula to find geometric mean for a grouped frequency distribution :

H = N/∑(f_i/x_i)

Fitting the given data in to the above formula, we get

= 10/(2/2 + 3/4 + 3/8 + 2/16)

= 10/(1 + 0.75 + 0.375 + 0.125)

= 10/2.25

= 4.44

From the given data calculate H.M 5, 10, 17, 24, 30

Harmonic mean = 5/(0.2 + 0.1 + 0.05 + 0.04 + 0.03)

= 5/0.42

= 11.9

So, the required harmonic mean is 11.9

Problem 4 :

If the arithmetic mean between two numbers is 64 and the geometric mean between them is 16. The harmonic mean between them is 

a)  64    b)  4     c)  16        d)  40

Solution :

Given that,

arithmetic mean = 64

Geometric mean = 16

(Geometric mean)² = Arithmetic mean x Harmonic mean

(16)² = 64 x Harmonic mean

Harmonic mean = 256/64

= 4

So, the required harmonic mean is 4.

Problem 5 :

If geometric mean is 6 and arithmetic mean is 6.5, then harmonic mean will be 

a) 6²/6.5     b)  6/6.5²    c)  6/6.5     d) None

Solution :

Given that,

arithmetic mean = 6.5

Geometric mean = 6

(Geometric mean)² = Arithmetic mean x Harmonic mean

6² = 6.5 x Harmonic mean

Harmonic mean = 36/6.5

= 5.53

So, the required harmonic mean is 5.5

Problem 6 :

A person purchases 5 dollars worth of eggs from 10 different markets. You are to find the average number of eggs per dollar purchases from all the markets taken together. The suitable average in this case s 

a)  Arithmetic mean      b) Geometric mean

c)  Harmonic mean      d)  None

Solution :

If rate are given so, we use Harmonic mean for suitable average.

Problem 7 :

______ is the reciprocal of the arithmetic mean of the reciprocal observations.

a)  Harmonic mean      b) Geometric mean

b)  Both a and b          d)  None

Solution :

Harmonic mean is the reciprocal of the arithmetic mean of the reciprocal observations.

Problem 7 :

The Harmonic mean A and B is 1/3 and Harmonic mean of C and D is 1/5. The harmonic mean of ABCD is 

a)  8/15    b)  1/4    c)  1/15    d)  5/3

Solution :

Harmonic mean of A and B = 1/3

Harmonic mean of C and D = 1/5

1/3 = 2/[(1/A) + 1/B)]

[(1/A) + 1/B)] = 6

1/5 = 2/[(1/C) + 1/D)]

[(1/C) + 1/D)] = 10 -----(2)

Harmonic mean of A, B, C and D

= 4/[(1/A) + 1/B)] + [(1/C) + 1/D)]

= 4/(6 + 10)

= 4/16

= 1/4

So, the required answer is 1/4.

Problem 8 :

A fire engine rushes to a place of fire accident with a speed of 110 kmph and after the completion of operation turned to the base at the speed of 35 kmph. The average speed per hour in per direction is obtained as _____ speeds.

a) Average of      b) Harmonic mean of 

c) Geometric mean of         d)  Hall of harmonic mean of

Solution :

Harmonic mean because if data are given in speed, distance and time we use Harmonic mean and 

average speed = 2xy/x + y

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.