HCF AND LCM OF DECIMALS
You can find highest common factor (HCF) or greatest common factor (GCF) and least common multiple (LCM) of two or more decimal numbers through the following steps.
Step 1 :
In the given decimal numbers, identify the number that has more number of digits after the decimal point and also count the number of digits after the decimal point.
For example, in 0.8 and 0.36, we have more number of digits after the decimal point in 0.36. That is 2.
Step 2 :
Multiply the decimal numbers by powers of 10 (10, 100, 1000.....) to get rid of the decimal point.
In 0.8 and 0.36, we have to multiply both the numbers by 100 to get rid of the decimal point.
Step 3 :
Find the HCF or LCM for the integers found in step 2.
That is, we have to find HCF or LCM for 80 and 36.
Step 4 :
Divide the HCF or LCM found in step 3 by the power of 10 that is multiplied in step 2.
HCF or LCM of 80 or 36 has to be divided by 100.
Example 1 :
Find the HCF of 0.12 and 0.16.
Solution :
In both 0.12 and 0.16, we have equal number of digits after the decimal point. That is 2.
Multiply both 0.12 and 0.16 by 100 to get rid of the decimal point.
0.12 x 100 = 12
0.16 x 100 = 16
Find the HCF of 12 and 16.
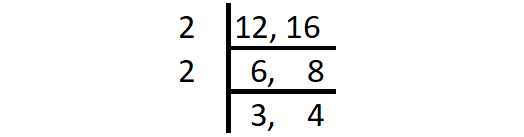
HCF (12, 16) = Product of common factors
= 2 x 2
= 4
Divide the HCF 4 by 100.
4/100 = 0.04
So, the highest common factor of 0.12 and 0.16 is
0.04
Example 2 :
Find the LCM of 0.8 and 0.12.
Solution :
In 0.8 and 0.12, we have more number of digits after the decimal point in 0.12. That is 2.
Multiply both 0.8 and 0.12 by 100 to get rid of the decimal point.
0.8 x 100 = 80
0.12 x 100 = 12
Find the LCM of 80 and 12.

LCM (80, 12) = Product of all prime factors
= 2 x 2 x 2 x 2 x 3 x 5
= 240
Divide the LCM 240 by 100.
240 / 100 = 2.4
So, the least common multiple of 0.8 and 0.12 is
2.4
Example 3 :
Find the HCF of 0.6, 0.75 and 1.05.
Solution :
In 0.6, 0.75 and 0.105, we have more number of digits after the decimal point in 0.75 and 1.05. That is 2.
Multiply the given numbers by 1000 to get rid of the decimal point.
0.6 x 100 = 60
0.75 x 100 = 75
1.05 x 100 = 105
Find the HCF of 60, 75 and 105.
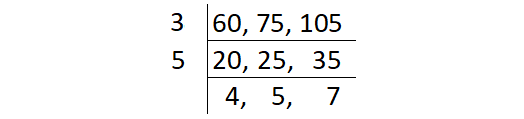
HCF (60, 75, 105) = Product of common factors
= 3 x 5
= 15
Divide the HCF 15 by 100.
15 / 100 = 0.15
So, the highest common factor of 0.6, 0.75 and 1.05 is
0.15
Example 4 :
Find the LCM of 0.48, 0.72 and 0.108.
Solution :
In 0.48, 0.72 and 0.108, we have more number of digits after the decimal point in 0.108. That is 3.
Multiply the given numbers by 1000 to get rid of the decimal point.
0.48 x 1000 = 480
0.72 x 1000 = 720
0.108 x 1000 = 108
Find the LCM of 480, 720 and 108.

LCM (480, 720, 108) = Product of all prime factors
= 2 x 2 x 3 x 2 x 2 x 5 x 3 x 2 x 3
= 4320
Divide the LCM 4320 by 1000.
4320 / 1000 = 4.32
So, the least common multiple of 0.48, 0.72 and 0.108 is
4.32
Example 5 :
Find the HCF and LCM of 0.6, 1.5, 0.18 and 3.6.
Solution :
In 0.6, 1.5, 0.18 and 3.6, we have more number of digits after the decimal point in 0.18. That is 2.
Multiply the given numbers by 100 to get rid of the decimal point.
0.6 x 100 = 60
1.5 x 100 = 150
0.18 x 100 = 18
3.6 x 100 = 360
Highest Common Factor :
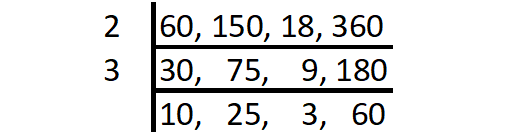
HCF (60, 150, 18, 360) = Product of common factors
= 2 x 3
= 6
Divide the HCF 6 by 100.
6 / 100 = 0.06
So, the highest common factor of 0.6, 1.5, 0.18 and 3.6 is
0.06
Least Common Multiple :
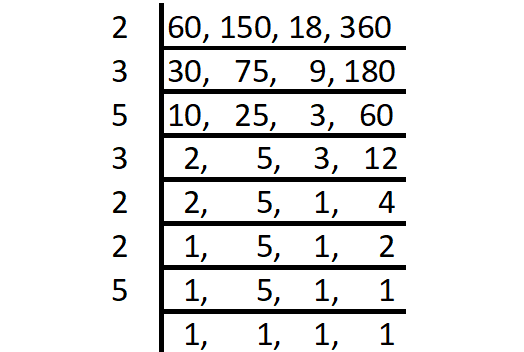
LCM (60, 150, 18, 360) = Product of all prime factors
= 2 x 3 x 5 x 3 x 2 x 2 x 5
= 1800
Divide the LCM 1800 by 100.
1800 / 100 = 18
So, the least common multiple of 0.6, 1.5, 0.18 and 3.6 is
18
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Resources (Videos, Concepts, Worksheets and More)
Feb 08, 25 10:15 PM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 107)
Feb 08, 25 10:13 PM
Digital SAT Math Problems and Solutions (Part - 107) -
Digital SAT Math Problems and Solutions (Part - 108)
Feb 08, 25 10:09 PM
Digital SAT Math Problems and Solutions (Part - 108)