HCF OF ALGEBRAIC EXPRESSIONS BY DIVISION METHOD

Sometimes the given polynomials are not factorable because of their highest powers. However, the following method gives a systematic way on finding HCF.

Step 1 :

Let " f(x) " and " g(x) " be the given polynomials. First, divide f(x) by g(x) to obtain, f(x) = g(x) x q(x) + r (x)

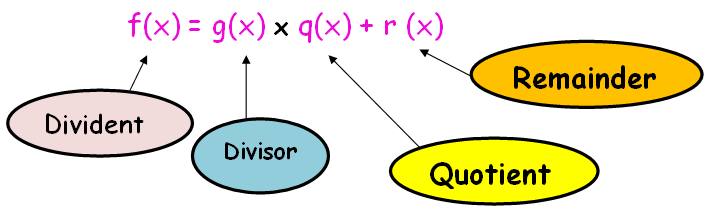
So, deg [ g(x) ] > deg [ r(x) ]. If remainder r (x) = 0, then g(x) is the HCF of given polynomials.  

Step 2 :

If the remainder r(x) is not zero, then divide g(x) by r(x) to obtain g(x) = r(x) x q(x) + r₁ (x).

Where  r₁ (x) is remainder. If it is zero, then r(x) is the required HCF. 

Step 2 :

If it is not zero, then continue the process until we get zero as remainder.

Question 1 :

Find the HCF of the following pairs of polynomials using division algorithm

x³ - 9 x² + 23 x - 15 ,  4 x² - 16 x + 12

Solution :

Let f (x) = x³ - 9 x² + 23 x - 15, g (x) = 4 x² - 16 x + 12

g (x)  =  4 (x² - 4 x + 3) 

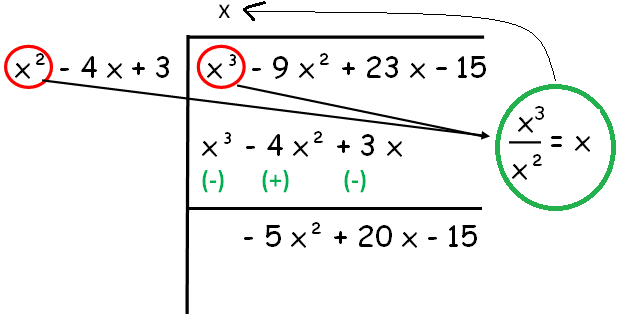
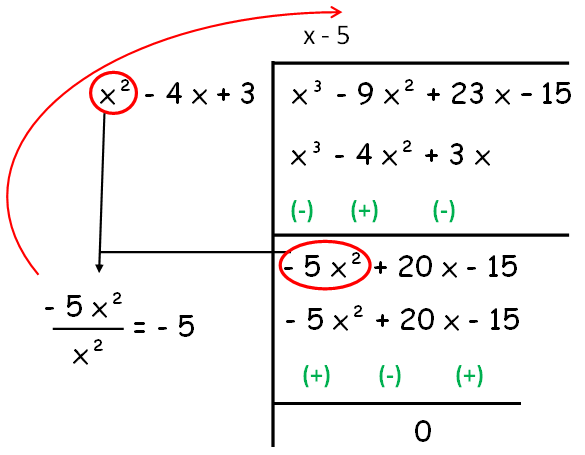
Since the remainder is 0, HCF of given polynomials is x - 5

Question 2 :

Find the HCF of the following pairs of polynomials using division algorithm

3 x³ + 18 x² + 33 x + 18 ,  3 x² + 13 x + 10

Solution:

f (x) = 3 x³ + 18 x² + 33 x + 18

g (x) = 3 x² + 13 x + 10

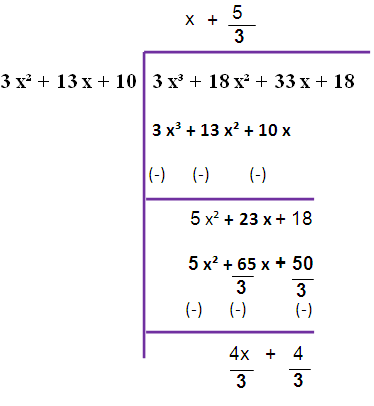
The remainder is not zero. So, we have to repeat this long division once again.

here r₁ (x) = (4/3)(x+1)

Now we are taking 4/3 as common from the remainder. So that we are getting (4/3)(x+1)

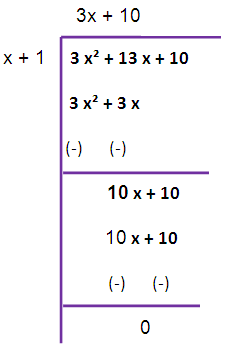
Therefore HCF is x + 1

Question 3 :

Find the HCF of the following pairs of polynomials using division algorithm

2 x³ + 2 x² + 2 x + 2 ,  6 x³ + 12 x² + 6 x + 12

Solution :

f (x) = 2 (x³ + x² + x + 1)

g (x) = 6 (x³ + 2 x² + x + 2)

We factor 2 from f (x) and 6 from g (x)

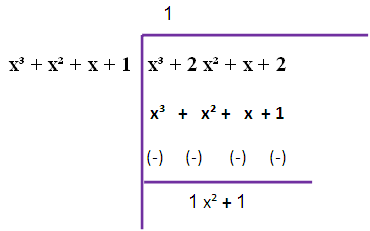
The remainder is not zero. So, we have to repeat this long division once again

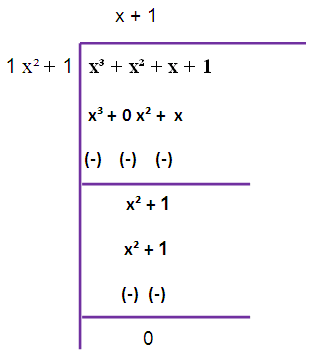
Therefore HCF is 2 (x² + 1)

Question 4 :

Find the HCF of the following pairs of polynomials using division algorithm

x³ - 3 x² + 4 x - 12 , x⁴ + x³ + 4 x² + 4 x

Solution :

f (x) = x³ - 3 x² + 4 x - 12

g (x) = x (x³ + x² + 4 x + 4)

We are taking x from g (x).

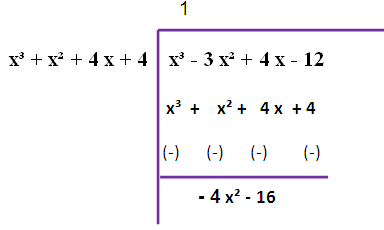
The remainder is not zero. So, we have to repeat this long division once again

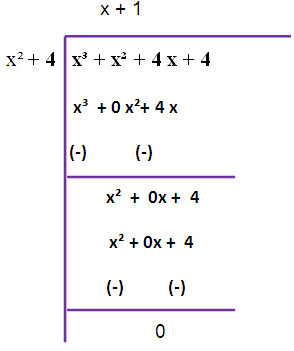
Therefore HCF is (x² + 4)

• HCF calculator
• HCF for algebraic expressions
• Venn diagram method for hcf and lcm
• Shortcut to find hcf and lcm
• How to solve hcf and lcm problems
• How to solve hcf and lcm word problems
• HCF and lcm worksheets
• Practical use of LCM
• LCM method for time and work
• LCM worksheet
• LCM calculator
• LCM and GCD worksheets

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.