HIGH SCHOOL MATH PROBLEMS WITH SOLUTIONS

Problem 1 :

Simplify the following

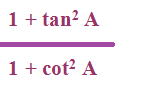
Solution :

L.H.S

  =  (1 + tan²A) / (1+cot²A)

sec²A - tan²A  =  1

sec²A  =  1 + tan²A

cosec²A - cot²A  =  1

cosec²A  =  1 + cot²A

  =  sec²A / cosec²A

  =  (1/cos²A) / (1/sin²A)

  =  sin²A/cos²A

  =  tan²A

Problem 2 :

From a point P on the ground the angle of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff  from P is 45°. Find the length of the flagstaff and the distance of the building from the point P. (take √3 = 1.732)

Solution :

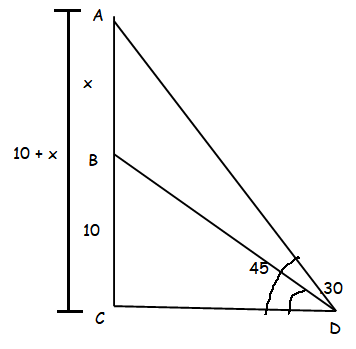
In triangle BCD,

tanθ  =  Opposite side / Adjacent side

tan 30  =  BC/CD

1/√3  =  10/CD

CD  =  10√3 ------(1)

In triangle ACD,

tan 45  =  AC/CD

1  =  (10 + x) /CD

CD  =  10 + x ------(2)

(1)  =  (2)

10√3  =  10 + x

x  =  10(√3 - 1)

x  =  10(10.732 - 1)

x  =  10(0.732)

x  =  7.32

The height of the flag staff is 7.32 m.

Problem 3 :

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower is 30°. Find the height of the tower.

Solution :

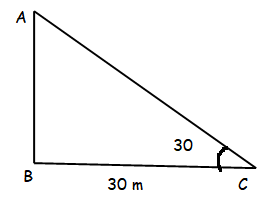
Height of the tower  =  AB, Distance between the foot of the tower and point of observation  =  BC.

tanθ  =  Opposite side / Adjacent side

tan θ  =  AB/BC

tan 30  =  AB/30

1/√3  =  AB/30

AB  =  30/√3

AB  =  (30/√3) ⋅ (√3/√3)

AB  =  30√3/3

AB  =  10√3

Problem 4 :

The coefficient of variation of a series is 69% and its standard deviation is 15. Find the mean.

Solution :

Coefficient of variation  =  (σ/x̅) ⋅ 100%

69/100  =  (15/x̅) ⋅ 100%

0.69  =  15/x̅

x̅  =  15/0.69

x̅  =  21.73

So, the required mean is 21.73.

Problem 5 :

If the two dice are thrown. what is the probability of getting the same number in both the dice.

Solution :

When two dice are thrown, the sample space

n(S)  =  36

Let A be the event of getting doublet.

A  =  { (1, 1) (2, 2) (3, 3) (4, 4) (5, 5) (6, 6) }

n(A)  =  6

p(A)  =  n(A)/n(S)

p(A)  =  6/36

Problem 6 :

2 cubes each of volume 64 cm³ are joined end to end. Determine the surface area of the resulting cuboid.

Solution :

Volume of one cuboid  =  64 cm³

a³  =  64

Side length of cube is 4 cm.

Side length of cuboid  =  4 + 4  =  8 cm

breadth  =  4 cm and height  =  4 cm

Surface area of cuboid  =  2(lb + bh + hl)

  =  2(8⋅4 + 4⋅4 + 4⋅8)

  =  2(32 + 16 + 32)

  =  2(80)

  =  160 cm²

Problem 7 :

A metallic sphere of radius 4.2 cm is melted and recast into a shape of a cylinder of radius 6 cm. Determine the height of the cylinder.

Solution :

Radius of sphere  =  4.2 cm

Radius of cylinder  =  6

Volume of sphere  =  Volume of cylinder

(4/3) πr³  =  πr² h

(4/3) 4.2³  =  6² h

h  =  98.784/36

h  =  2.744

So, the height of the cylinder is 2.744 cm.

Problem 8 :

The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Determine the curved surface area of the frustum.

Solution :

Slant height (l)  =  4 cm

Circumference of larger circle  =  18

Surface area of the frustum cone  =  πl (R + r)

  =  π ⋅ 6(9/π + 3/π)

  =  6(9+3)

  =  12(6)

  =  72

Problem 9 :

Find the HCF of 96 and 404 by the prime factorization method. Find their LCM.

Solution :

  =  2 ⋅ 2

  =  4

Problem 10 :

The angle in a semi circle is

Solution :

Angle in a semi circle is right angle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.