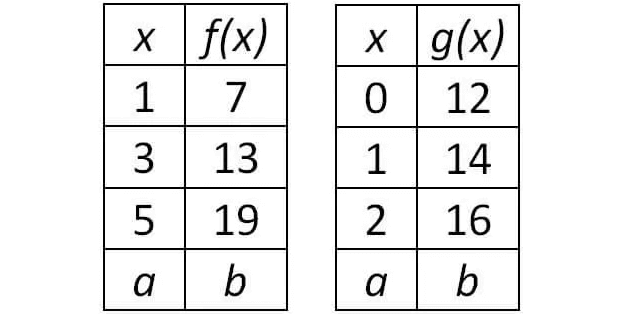HIGH SCHOOL MATH QUESTIONS WITH ANSWERS

Problem 1 :

Find the centroid of the triangle whose vertices are the points A (8 , 4) B (1 , 3) and C (3 , -1).

Solution :

Centroid of the triangle  =  (x₁ +x₂ + x₃)/3, (y₁+y₂+y₃)/3

  =  (8+1+3)/3, (4+3-1)/3

  =  12/3, 6/3

  =  (4, 2)

So, the centroid of the triangle is (4, 2).

Problem 2 :

If the two lines are perpendicular with the slopes m₁ and m₂ then m₁ ⋅ m₂ =

Solution :

If two lines are perpendicular, then the product of their slopes will be equal to -1.

Problem 3 :

Find the coordinates of the orthocenter of the triangle whose vertices are A(3, 1), B(0, 4) and C(-3, 1).

Solution :

The point of intersection of two perpendicular drawn from any two vertices of the triangle is known as orthocenter.

Let us consider the perpendicular drawn from A is AD and perpendicular drawn from the vertex B is BE.

Slope of AC  =  [(y₂ - y₁)/(x₂ - x₁)]

A (3, 1) and C (-3, 1)

here x₁  =  3, x₂  =  -3, y₁  =  1 and y₂  =  1

  =  (1 - 1) / (-3 - 3)

=  0 / (-6)

=  0

Slope of the altitude BE  =  -1/ slope of AC

  =  -1/0

Equation of the altitude BE :

(y - y₁)  =  m (x -x₁)

Here B (0, 4) and m  =  -1/0

 (y - 4)  =  -1/0 (x - 0)

10 (y - 4)  =  -1(x)

x + 10y - 40  =  0  --------(1)

Slope of BC  =  (y₂ - y₁)(x₂ - x₁)]

B (0, 4) and C (-3, 1)

Here x₁ = 0, x₂ = -3, y₁ = 4 and y₂ = 1.

  =  (1 - 4) / (-3 - 0)

  =  (-3)/(-3)

   =  1

Slope of the altitude AD  =  -1/ slope of AC

=  -1/1

=  -1

Equation of the altitude AD :

(y - y₁)  =  m (x - x₁)

Here A(3, 1)  m  =  -1

(y - 1)  =  -1 (x - 3)

(y - 1)  =  -x + 3

x + y - 1 - 3  =  0

x + y - 4  =  0

x = -y + 4--------(2)

Substituting (2) into (1), we get

-y + 4 + 10y - 40  =  0

9y - 36  =  0

y  =  36/9

y  =  4

By applying y  =  4 in (1), we get

x  =  -4 + 4

x  =  0

Therefore the orthocenter is (0, 4).

Problem 4 :

Sum of the areas of two squares is 468 m². If the difference of their perimeters is 24 m, determine the sides of the two squares.

Solution :

Let x and y be the side length of squares.

x² + y²  =  468  ----(1)

4x - 4y  =  24 

x - y  =  6

x  =  6 + y ----(2)

(6+y)² + y²  =  468 

36+y²+12y+y²-468  =  0 

2y² + 12y - 432  =  0

y² + 6y - 216  =  0

(y - 12)(y + 18)  =  0

y  =  12 and y  =  -18 (not admissible)

If y =  12, then x  =  18

So, the side length of required squares are 12 and 18 respectively.

Problem 5 :

Two concentric circles are of radii 5 cm and 3 cm. Determine the length of the chord of the larger circle which touches the smaller circle.

Solution :

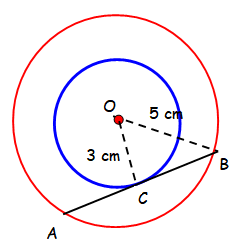
In triangle OCB,

OB²  =  OC² + BC²

5²  =  3² + BC²

BC²  =  25 - 9

BC²  =  16

BC  =  4

Problem 6 :

If sin A = 3/4, then the value of tan A

Solution :

Given, 

sin A = 3/4  =  Opposite side/Hypotenuse

Adjacent side²  =   Hypotenuse² - Opposite side²

Adjacent side²  =   4² - 3²

Adjacent side²  =  16 - 9

Adjacent side  = √7

 tan A  =  Opposite side / Adjacent side

 tan A  =  3/√7

Problem 7 :

In triangle PQR right-angled at Q , PQ = 3 cm and PR = 6 cm. Determine ∠QPR

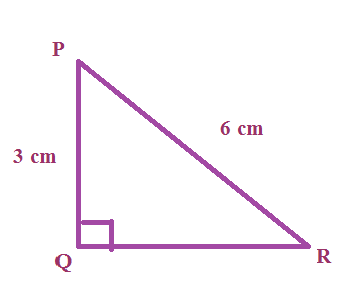
Solution :

tan p  =  Opposite side / Adjacent side

Using Pythagorean theorem,

PR² = PQ² + QR²

6² = 3² + QR²

36 - 9 = QR²

QR² = 27

QR = 3√3

tan p  =  PQ/QR

tan p  =  3/√3

Multiplying both numerator and denominator by √3, we get

tan p  =  √3

 ∠QPR = 60°

Problem 8 :

Simplify the following.

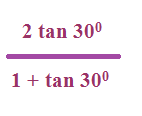
Solution :

  =  2tan 30 / (1 + tan 30)

  =  2 (1/√3) / (1 + 1/√3)

  =  2/(√3 + 1)

  =  2/(√3 + 1) ⋅ [(√3 - 1)/(√3 - 1)]

  =  2(√3 - 1)/(√3² - 1)

  =  2(√3 - 1)/2

  =  √3 - 1

Problem 9 :

Evaluate the following

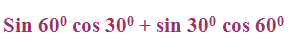
Solution :

sin60 cos30 + sin30 cos60

  =  √3/2 (√3/2) + (1/2)(1/2)

  =  3/4 + 1/4

  =  4/4

  =  1

Problem 10 :

Simplify (sec A + tan A)  (1 - sin A) =

Solution :

(sec A + tan A)  (1 - sin A)

  =  (1/cos A + sin A/cos A) (1-sinA)

  =  [(1+sinA)/cos A] ⋅(1-sinA)

  =  (1 - sin²A)/cos A

  =  cos²A/cos A

  =  cos A

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.