HORIZONTAL AND VERTICAL ASYMPTOTES OF RATIONAL FUNCTIONS
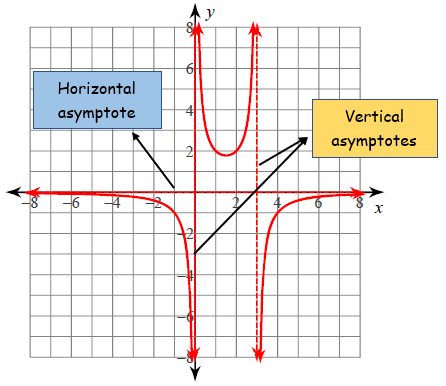
Vertical Asymptote :
The vertical line x = a is called a vertical asymptote of the graph of y = f(x) if
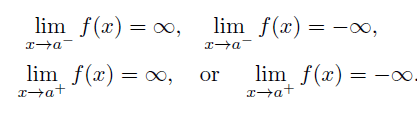
How to find vertical asymptote?
The graph of y = f(x) will have vertical asymptotes at those values of x for which the denominator is equal to zero.
Horizontal Asymptote :
The horizontal line y = b is called a horizontal asymptote of the graph of y = f(x) if either The graph of y = f(x) will have at most one horizontal asymptote. It is found according to the following :
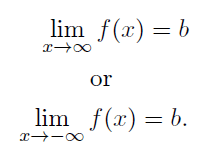
How to find vertical and horizontal asymptotes of rational function?
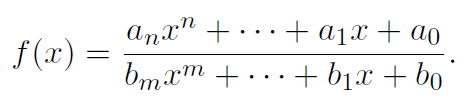
How to find horizontal asymptote?
1) If
degree of numerator > degree of denominator
then the graph of y = f(x) will have no horizontal asymptote.
2) If
degree of numerator = degree of denominator
then the graph of y = f(x) will have a horizontal asymptote at y = an/bm.
3) If
degree of numerator < degree of denominator
then the graph of y = f(x) will have a horizontal asymptote at y = 0 (i.e., the x-axis).
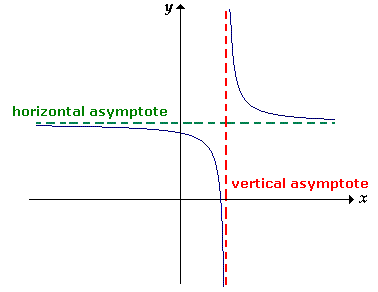
- A graph can have an infinite number of vertical asymptotes, but it can only have at most two horizontal asymptotes.
- Horizontal asymptotes describe the left and right-hand behavior of the graph.
- A graph will (almost) never touch a vertical asymptote; however, a graph may cross a horizontal asymptote.
Find the vertical and horizontal asymptotes of the functions given below.
Example 1 :
f(x) = -4/(x2 - 3x)
Solution :
Vertical asymptotes :
x2 - 3x = 0
x(x-3) = 0
x = 0 and x = 3
So, the vertical asymptotes are x = 0 and x = 3.
Horizontal asymptotes :
Comparing highest exponents,
denominator > numerator
So, horizontal asymptote is at y = 0.
Example 2 :
f(x) = (x-4)/(-4x-16)
Solution :
Vertical asymptotes :
-4x-16 = 0
-4(x+4) = 0
x = -4
So, vertical asymptote is x = -4.
Horizontal asymptotes :
Comparing highest exponents,
denominator = numerator
Horizontal asymptote
= Coefficient of x of numerator/Coefficient of x in the denominator
y = -1/4
So, horizontal asymptote is y = -1/4.
Example 3 :
f(x) = (x+4)/(-2x-6)
Solution :
Vertical asymptotes :
-2x-6 = 0
-2x = 6
x = -3
So, vertical asymptote is x = -3.
Horizontal asymptotes :
Comparing highest exponents,
denominator = numerator
Horizontal asymptote
= Coefficient of x of numerator/Coefficient of x in the denominator
y = -1/2
So, horizontal asymptote is y = -1/2.
Example 4 :
f(x) = (x3-9x)/(3x2-6x-9)
Solution :
Vertical asymptotes :
3x2-6x-9 = 0
3(x2-2x-3) = 0
(x-3)(x+1) = 0
x = 3 and x = -1
So, vertical asymptotes are x = 3 and x = -1.
Horizontal asymptotes :
Comparing highest exponents,
numerator > denominator
So, there is no horizontal asymptote.
Example 5 :
f(x) = (3x2-12x)/(x2-2x-3)
Solution :
Vertical asymptotes :
x2-2x-3 = 0
(x-3)(x+1) = 0
x = 3 and x = -1
So, vertical asymptotes are x = 3 and x = -1.
Horizontal asymptotes :
Comparing highest exponents,
numerator = denominator
coefficient of x from the numerator/coefficient of x in the denominator
y = 3/1
y = 3
So, the horizontal asymptote is y = 3.
Example 6 :
f(x) = (x3-16x)/(-4x2+4x+24)
Solution :
Vertical asymptotes :
-4x2+4x+24 = 0
-4(x2-x-6) = 0
(x-3)(x+2) = 0
x = 3 and x = -2
Horizontal asymptotes :
Comparing highest exponents,
numerator > denominator
So, there is no horizontal asymptote.
Example 7 :
f(x) = (x2+2x)/(-4x+8)
Solution :
Vertical asymptotes :
-4x+8 = 0
-4(x-2) = 0
x = 2
So, vertical asymptote is x = 2.
Horizontal asymptotes :
Comparing highest exponents,
numerator > denominator
So, there is no horizontal asymptote.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 134)
Apr 02, 25 12:40 AM
Digital SAT Math Problems and Solutions (Part - 134) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Apr 02, 25 12:35 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part 135)
Apr 02, 25 12:32 AM
Digital SAT Math Problems and Solutions (Part 135)

