HOW MANY NUMBERS ARE THERE BETWEEN 1 AND 1000
Question 1 :
To travel from a place A to place B, there are two different bus routes B1,B2, two different train routes T1, T2 and one air route A1. From place B to place C there is one bus route say B'1, two different train routes say T'1, T'2 and one air route A'1. Find the number of routes of commuting from place A to place C via place B without using similar mode of transportation.
Solution :
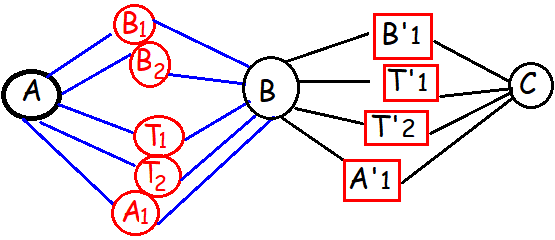
CASE 1 :
If we choose the transportation bus from place A to B, we have to choose either train or air, to go from B to C.
- If we choose B1, we will have 3 ways (T1', T2', A1')
- If we choose B2, we will have 3 ways (T1', T2',A1')
= 3 + 3 = 6 ways
CASE 2 :
If we choose the transportation train from place A to B, we have to choose either bus or air, to go from B to C.
- If we choose T1, we will have 2 ways (B1', A1')
- If we choose T2, we will have 2 ways (B1', A1')
= 2 + 2 = 4 ways
CASE 3 :
If we choose the transportation air from place A to B, we have to choose either bus or train, to go from B to C.
- If we choose A1, we will have 3 ways (B1', T1', T2')
Hence total number of routes = 6 + 4 + 3
= 13 ways
Question 2 :
How many numbers are there between 1 and 1000 (both inclusive) which are divisible neither by 2 nor by 5?
Solution :
We may form one digit, two digit and three digit numbers from 1 to 1000.
One digit numbers not divisible by 2 and 5
The numbers 1, 3, 7 and 9 are not divisible by both 2 and 5.
= 4 numbers
Two digit numbers not divisible by 2 and 5
Since the required numbers are not divisible by bot 2 and 5, it ends with (1, 3, 7, 9)
Unit digit :
We have 4 options
Tens digit :
Other than 0, we have 9 options
= 9 ⋅ 4 = 36 numbers
Three digit numbers not divisible by 2 and 5
Since the required numbers are not divisible by bot 2 and 5, it ends with (1, 3, 7, 9)
Unit digit :
We have 4 options
Hundreds digit :
Other than 0, we have 9 options
Tens digit :
Including 0, we have 10 options
= 10 ⋅ 9 ⋅ 4 = 360 numbers
Hence total number to be formed = 4 + 36 + 360
= 400 numbers
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 62)
Nov 05, 24 11:16 AM
Digital SAT Math Problems and Solutions (Part - 62) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Nov 05, 24 11:15 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Worksheet on Proving Trigonometric Identities
Nov 02, 24 11:58 PM
Worksheet on Proving Trigonometric Identities
