HOW TO CALCULATE LENGTH OF CHORD IN CIRCLE

Example 1 :

A chord is 8 cm away from the center of a circle of radius 17 cm. Find the length of the chord.

Solution :

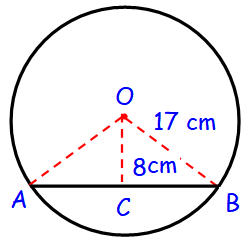
Here the line OC is perpendicular to AB, which divides the chord of equal lengths.

In Δ OCB,

OB²  =  OC² + BC²

17²  =  8² + BC²

BC²  =  17² - 8²

BC  =  √(17² - 8²)

BC  =  √289 - 64

BC  =  √225

BC  =  √(15 ⋅ 15)

BC  =  15 cm

Length of chord  =  AB  =  2 (Length of BC)

  =  2 (15)

=  30 cm

Hence the length of chord is 30 cm.

Example 2 :

Find the length of a chord which is at a distance of 15 cm from the center of a circle of radius 25 cm.

Solution :

Distance of chord from center of the circle  =  15 cm

Radius of the circle  =  25 cm

Length of chord  =  AB

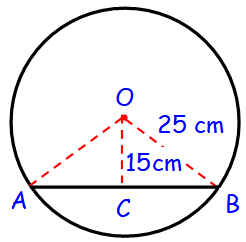
Here the line OC is perpendicular to AB, which divides the chord of equal lengths.

In Δ OCB,

OB²  =  OC² + BC²

25²  =  15² + BC²

BC²  =  25² - 15²

BC  =  √(25² - 15²)

BC  =  √625 - 225

BC  =  √400

BC  =  √(20 ⋅ 20)

BC  =  20 cm

Length of chord  =  AB  =  2 (Length of BC)

  =  2 (20)

=  40 cm

Hence the length of chord is 40 cm.

Example 3 :

A chord of length 20 cm is drawn at a distance of 24 cm from the center of a circle. Find the radius of the circle.

Solution :

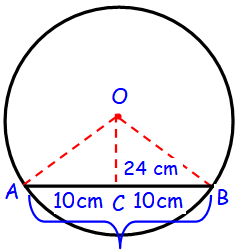
Here the line OC is perpendicular to AB, which divides the chord of equal lengths.

In Δ OCB,

OB²  =  OC² + BC²

OB²  =  24² + 10²

BC²  =  576 + 100

BC²  =  676

BC  =  √676

BC  =  √(26 ⋅ 26)

BC  =  26  cm

Hence the radius of the circle is 26 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.