HOW TO CHECK CONSISTENCY OF LINEAR EQUATIONS USING MATRICES

Test for consistency and if possible, solve the following systems of equations by rank method.

Question 1 :

2x + y + z = 5

x + y + z = 4

x - y + 2z = 1

Solution :

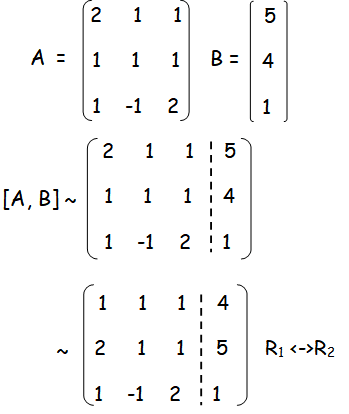
Number of non zero rows are 3.

ρ(A) = ρ([A|B]) = 3. The system is consistent and it has unique solution.

From 1^st row,

x + y + z  = 4 -----(1)

From 2^nd row,

-y-z  =  -3 -----(2)

From 3^rd row,

3z  =  3 -----(3)

From (3)

z  =  1

By applying the value of z in (2), we get

-y-1  =  -3

-y  =  -3+1

-y  =  -2 and y  =  2

By applying the value of y and z in (1), we get

x + 2 + 1  =  4

x  =  4-3

x  =  1

x  =  1, y  =  2 and z  =  1

Question 2 :

x + 2y + z = 7

2x - y + 2z = 4

x + y - 2z = -1

Solution :

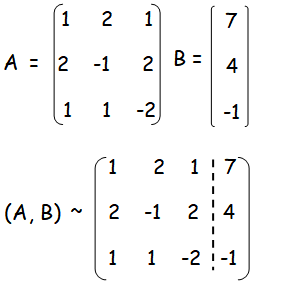
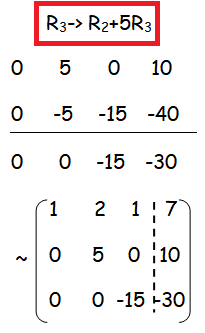
Number of non zero rows are 3.

ρ(A) = ρ([A|B]) = 3. The system is consistent and it has unique solution.

From the 1^st row,

x+2y+z  =  7  ----(1)

From the 2^nd row,

5y  =  10  ----(2)

y  =  2

From the 3^rd row,

-15z  =  -30   ----(3)

z  =  2

By applying the value of y and z in (1), we get

x + 2(2) + 2 = 7

x + 6 = 7

x = 7 - 6

x = 1

x  =  1, y  =  2 and z  =  2

Question 3 :

x + 9y - z = 27

x - 8y + 16z = 10

2x + y + 15z = 37 

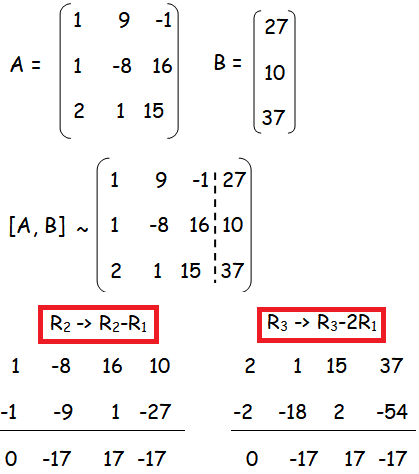
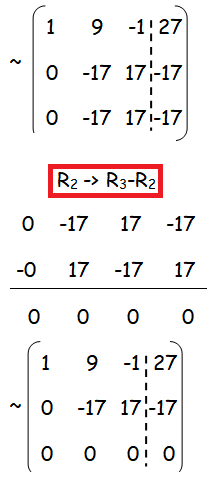
Here ρ(A) = ρ([A|B]) = 2 < 3, then the system is consistent and it has infinitely many solution.

From the 1^st row,

x + 9y-z  =  27    ---(1)

From the 2^nd row,

17y + 17z  =  -17   ---(2)

Dividing by 17, we get

y + z  =  -1

Put z  =  t

y  =  -1 - t

By applying the value of y and z in (1), we get

x + 9(-1 - t) - t = 27

x - 9 + 9t - t = 27

x = 27 + 9 - 8t

x = 36 - 8t

x = 36 - 8t, y = -1 - t and z = t where t ∈ Real numbers.

Question 4 :

x + y + z = 3

3x + 2y + z = 3

-x - y - z = 1

Solution :

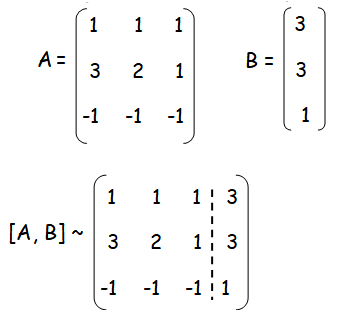
Here ρ(A)  =  2,  ρ([A|B])  =  3

ρ(A) ≠ ρ([A|B]) then the system is inconsistent and it has no solution.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.