HOW TO CHECK IF THE FUNCTION IS ONE TO ONE FROM ITS GRAPH

A function is one-to-one if and only if every horizontal line intersects the graph of the function in at most one point.

When using the horizontal line test, be careful about its correct interpretation: If you find even one horizontal line that intersects the graph in more than one point, then the function is not one-to-one.

However, finding one horizontal line that intersects the graph in at most one point does not imply anything concerning whether or not the function is one-to-one. For the function to be one-to-one, every horizontal line must intersect the graph in at most one point.

Question 1 :

Suppose f is the function with domain [1, 4] whose graph is shown here in the margin. Is f a one to one function ?

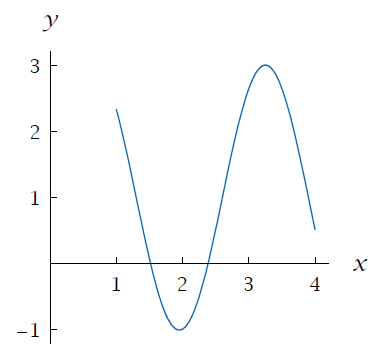
Solution :

Let us draw a line passes through y - axis.

The line y = 2 intersects the graph of f in three points. Thus there are three numbers x in the domain of f such that f(x) = 2. 

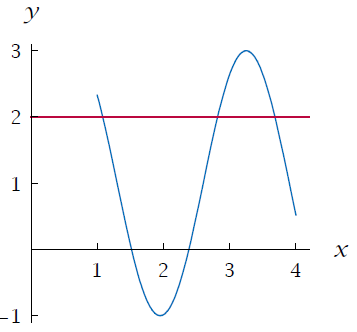
The vertical line intersects the graph more than 1 point. Hence f is not a one-to-one function.

Question 2 :

f is the function with domain [−2, 2] whose graph is shown here in the margin. Is f a one to one function ?

Solution :

Let us draw the line y = 1 and y = 3.

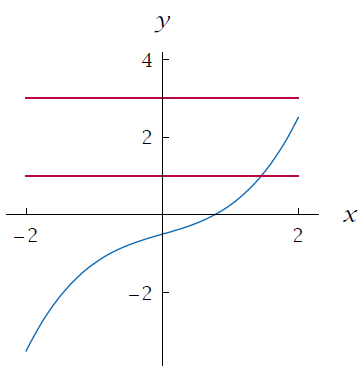
The line y = 1 intersects the graph of f in one point, and the line y = 3 intersects the graph in zero points. Furthermore, we can see from the figure that each horizontal line will intersect the graph in at most one point. Hence f is a one-to-one function.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.