HOW TO CHECK IF THE GIVEN FOUR POINTS FORM A RHOMBUS

(i) Find the length of all sides using the formula distance between two points.

(ii) In any square the length of diagonal will be equal, to prove the given shape is not square but a rhombus, we need to prove that length of diagonal are not equal.

Question 1 :

Examine whether the given points A (2,-3) and B (6,5) and C (-2,1) and D (-6,-7) forms a rhombus.

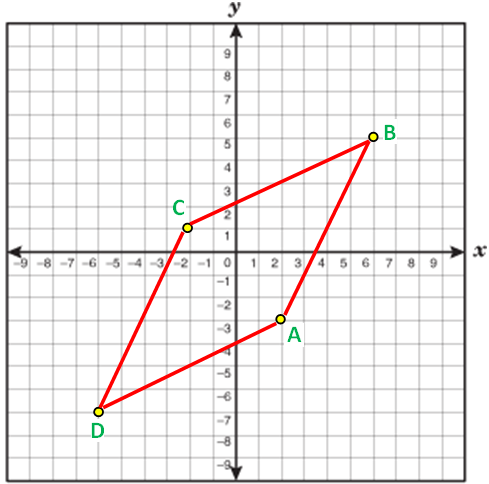
Solution :

Distance Between Two Points (x ₁, y₁) and (x₂ , y₂)

√(x₂ - x₁)² + (y₂ - y₁)²

Four points are A (2,-3) and B (6,5) and C (-2,1) and D (-6,-7)

Distance between the points A and B :

Here x₁ = 2, y₁ = -3, x₂ = 6  and  y₂ = 5

=    √(6-2)² + (5-(-3))²

=    √(4)² + (5+3)²

=    √16 + 8²

=    √16 + 64

=     √80 units

Distance between the points B and C :

Here x₁ = 6, y₁ = 5, x₂ = -2  and  y₂ = 1

=    √(-2-6)² + (1-5)²

=    √(-8)² + (-4)²

=    √64 + 16

=    √80 units

Distance between the points C and D :

Here x₁ = -2, y₁ = 1, x₂ = -6  and  y₂ = -7

=    √(-6-(-2))² + (-7-1)²

=    √(-6+2)² + (-8)²

=    √(-4)² + 64

=    √16 + 64

=    √80 units

Distance between the points D and A :

Here x₁ = -6, y₁ = -7, x₂ = 2  and  y₂ = -3

=    √(2-(-6))² + (-3-(-7))²

=    √(2+6)² + (-3+7)²

=    √8² + 4²

=   √64 + 16

=   √80 units

AB = √80 units

BC = √80 units

CD = √80 units

DA = √80 units

Length of diagonal AC :

Here x₁ = 2, y₁ = -3, x₂ = -2  and  y₂ = 1

=    √(-2-2)² + (1-(-3))²

=    √(-4)² + (1+3)²

=    √16 + 4²

=    √16 + 16

=    √32 units

Length of diagonal BD :

Here x₁ = 6, y₁ = 5, x₂ = -6  and  y₂ = -7

=    √(-6-6)² + (-7-5)²

=    √(-12)² + (-12)²

=    √144 + 144

=    √288 units

Since the lengths of diagonals are not equal, the given vertices will form a rhombus.

Try other questions

(2)  Examine whether the given points A (1,4) and B (5,1) and C (1,-2) and D (-3,1) forms a rhombus.     Solution

(3)  Examine whether the given points A (1,1) and B (2,1) and C (2,2) and D (1,2) forms a rhombus.    Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.