HOW TO CHECK IF THE GIVEN NUMBER IS PERFECT CUBE OR NOT

To check if the given number is perfect cube or not, we use the method called prime factorization.

After grouping the factors as triples, if we have numbers remaining. Then we may decide that the given number is not a perfect cube.

Let us look into some examples to understand howto check the given number is perfect cube or not.

Example 1 :

Is 500 a perfect cube ?

Solution :

500  =  2 ⋅ 2 ⋅ 5 ⋅ 5 ⋅ 5

There are three 5’s in the product but only two 2’s.

Hence 500 is not perfect cube.

Example 2 :

Is 64 a perfect cube ?

Solution :

64  =  2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2

We may group 2 as triples.

Hence 64 is a perfect cube.

Example 3 :

Is 400 a perfect cube ?

Solution :

400  =  2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5

In the product, we have four 2's and two 5's.

After grouping 2's as triples, we left over with one 2 and two 5's.

Hence 400 is not perfect cube.

Example 4 :

Is 216 a perfect cube ?

Solution :

216  =  2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3

In the product, we have three 3's and three 2's.

After grouping 2 and 3 as triples, we don't have any remaining numbers. 

Hence 216 is perfect cube.

Example 5 :

Is 900 a perfect cube ?

Solution :

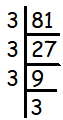
81  =  3 ⋅ 3 ⋅ 3 ⋅ 3

In the product, we have four 3's.

After grouping 3 as triples, we left over with one 3.

Hence 81 is perfect cube.

Example 6 :

Is 1000 a perfect cube ?

Solution :

1000  =  10 ⋅ 10 ⋅ 10

We may decompose 1000 as the product of three same numbers.

Hence 1000 is perfect cube.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.