HOW TO CHECK IF THE GIVEN RELATION IS FUNCTION

Problems 1-2 : State whether the following relations are functions or not. If it is a function, check for one-to-one onto. If it is not a function, state why?

Problem 1 :

A = {a, b, c} and f = {(a, c), (b, c), (c, b)}; (f : A ---> A).

Solution :

In order to check, if the given relation form a function, it has to satisfy the following conditions.

(i) Domain of f = {a, b, c} = set A.

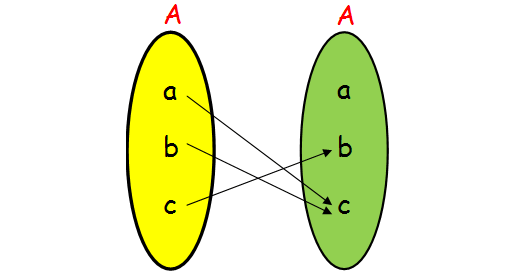
(ii)  For each x ∊ A, there is only one y ∊ A. Hence it is a function.

Not One to One :

If it is one to one function, then each elements of A will be associated with different elements of A. Here the elements a and b are associated with c.

Not Onto :

The element a is not associated with any of the elements, hence it is not onto.

Problem 2 :

If X = {x, y, z} and f = {(x, y), (x, z), (z, x)}; (f : X ---> X).

Solution :

(i)  Domain of f  =  {x, z}  ≠ set X

Hence it is not a function.

Problem 3 :

Let A = {1, 2, 3, 4} and B = {a, b, c, d}.

Give a function from A ---> B for each of the following :

(i) neither one-to-one nor onto.

(ii) not one-to-one but onto.

(iii) one-to-one but not onto.

(iv) one-to-one and onto.

Solution :

(i) neither one-to-one nor onto.

First let us draw a arrow diagram under the given condition, then write the relation from the arrow diagram.

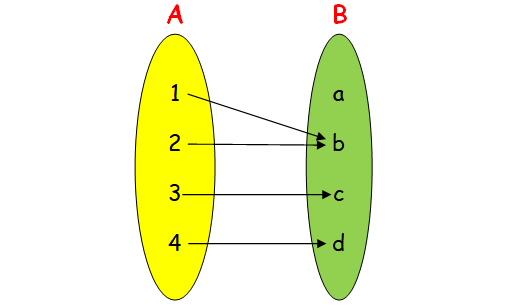
It is not one to one, because 1 and 2 are having same image b.

It is not onto, because a is not having preimage.

Hence the required relation is {(1, b) (2, b) (3, c) (4, d)}

(ii) not one-to-one but onto.

Inorder to prove it is an onto function, every element of B should have atleast one preimage. If we associate each elements of B with A, we will get one to one function or not a function. 

Hence it is not possible.

(iii) one-to-one but not onto

To prove it is an one to function, we need to associate every element of A with different elements of B. By doing this we will not get onto function. Hence it is not possible.

(iv) one-to-one and onto.

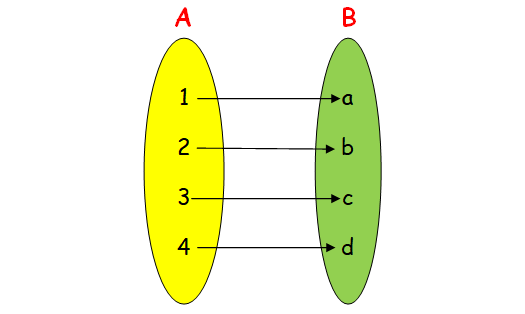
To prove it is an one to function, we need to associate every element of A with different elements of B. It is also an onto function.

Hence the required relation is {(1, a) (2, b) (3, c) (4, d)}.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.